LinMap: Visualizing Complexity Gradients in Evolutionary Landscapes [1]
Abstract
This article describes an interactive visualization tool, LinMap, for exploring the structure of complexity gradients in evolutionary landscapes. LinMap is a computationally efficient and intuitive tool for visualizing and exploring multidimensional parameter spaces. An artificial cell lineage model is presented that allows complexity to be quantified according to several different developmental and phenotypic metrics. LinMap is applied to the evolutionary landscapes generated by this model to demonstrate that different definitions of complexity produce different gradients across the same landscape; that landscapes are characterized by a phase transition between proliferating and quiescent cell lineages where both complexity and diversity are maximized; and that landscapes defined by adaptive fitness and complexity can display different topographical features.
|
|
|
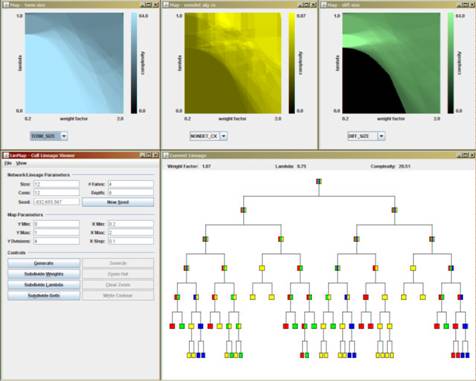
Figure 4: An example screenshot from LinMap. The three heat map panels along the top indicate different complexity gradients in the same evolutionary landscape. The cell lineage panel illustrates the currently selected developmental system. Selecting a location on the heat map causes the corresponding cell lineage to be displayed. The control panel in the lower left allows various genotypic and developmental parameters to be adjusted, control of sampling resolution and enlargement, and the saving and loading of generated landscapes. |
Tutorial material: Critical regions require recursive subdivisions of parameter spaces
Excerpt from Section 4 Visualizing and Exploring Evolutionary Space [1] (see also [3])
�Questions that cannot be answered using a statistical approach include:
� Where in a parameter space are complex behaviors likely to be located?
� How uniform is the distribution of complexity across a parameter space?
� What shape do complexity thresholds take?
� What types of phenotypes are located around a particular point in an evolutionary landscape?
� How are the complexity gradients in a landscape correlated with adaptive gradients?
� And finally, what do the members of these statistical ensembles actually look like?
To address these questions, we designed a visualization tool, LinMap, that enabled the micro-scale structure of an evolutionary landscape to be explored interactively.�
Complex systems often have regions of parameter space where tiny parameter changes cause major shifts in overall behavior, and other regions where major parameter shifts cause very little behavioral change. Critical regions are often of interest for investigation and control. Think about the stability of an airplane in flight. You could bump the plane�s surfaces almost everywhere and the trajectory would change infinitesimally.� But tiny changes to the throttle can cause major changes in the plane�s flight path. In evolutionary computation, such critical regions genomes can show radical changes in evolutionary forms.
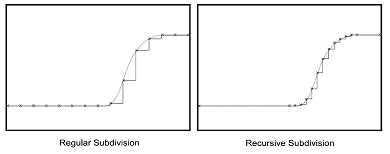
When investigating the behaviors of complex systems, uniform sampling of parameter spaces (see Figure left panel) produces few samples in transition regions.� Recursive subdivision (Figure right panel) automatically samples the transition regions which have the highest variability.
|
|
|
Figure 5. Reconstructed functions generated by regular and recursive subdivision and sampling. In both cases, 15 sample system behaviors have been generated. Recursive subdivision automatically produces increased sampling resolution in the heterogeneous transitional region and a reduced level of sampling in the homogeneous regions. (for algorithm details see [3]) |
|
|
|
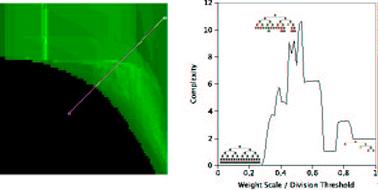
Figure 10: The complexity contour generated by taking a cross-section through space (N = 12;K = 12; lamdba = [0; 1:0];W = [0:1; 2:0]). At low values of W and lamdba, cells proliferate inde |
References
[1] N Geard and J Wiles (2008) LinMap: Visualizing Complexity Gradients in Evolutionary Landscapes, Artificial Life 14(3):277-297� (doi:10.1162/artl.2008.14.3.14304) .� PDF(453.577 KB) PDF Plus(483.071 KB)
[2] http://itee.uq.edu.au/~nic/_linmap/
[3] N Geard (2006) Two Design Patterns for Visualising the Parameter Space of Complex Systems, ACCS Technical Report, University of Queensland, November 9, 2006. PDF