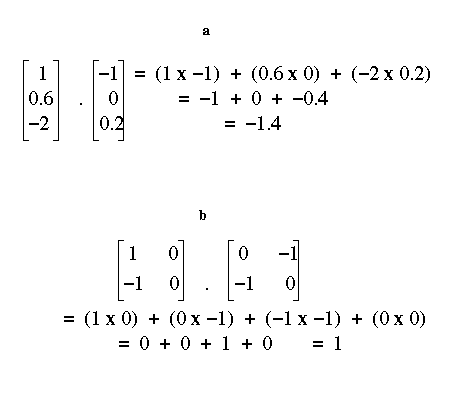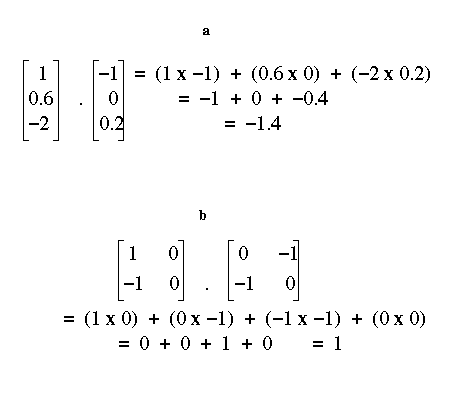[Previous] [Next]

Operations on Vectors: Dot Product

A Dot Product is calculated by multiplying together the values which are in the same position within the two vectors, and then adding the results of these multiplications together to get a scalar (see Figure 6a). In the case of the neural network, this involves multiplying each input unit activation by the corresponding weight value and then adding. The dot product of two vectors represents the level of similarity between them and can be extended to higher rank tensors (see figure 6b)

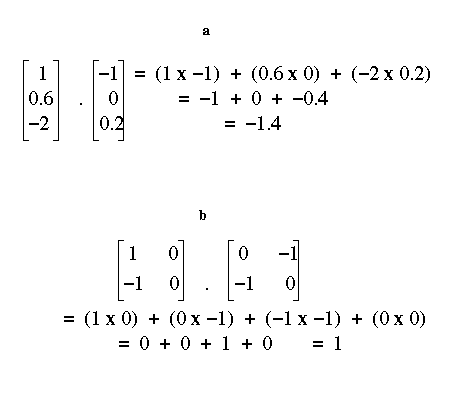
Figure 6: The Dot Product.

The dot product is expressed algebraically as a dot, that is, the dot product of the vectors v and w is written v.w.

If the dot product of two vectors is zero (v.w = 0) then the vectors are orthogonal.

If the dot product of a vector and itself is 1 then the vector is normal.

More generally, the dot product of a vector and itself is the length of the vector squared:
x.x = |x|²