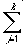[Table of Contents]

The Matrix Model: A Tutorial

Jill White
Simon Dennis

Contents

• Introduction
  • Memory Representations
  • Accessing Memory Representations
• Mathematical Model
  • Symbols
  • Vectors
  • Dot Products
  • Matrix Products
  • Pre-existing Memories
• Recognition
• Cued Recall with a List Associate
• Matrix Model Tutorial Questions

Introduction

The Matrix Model of Memory was developed by Humphreys, Bain and Pike (1989) and Pike (1984) to provide a coherent theoretical account of a range of different memory tasks, including episodic tasks, such as recognition and recall, and semantic tasks, such as familiarity rating and indirect production tasks. It comprises a distributed associative model in which items are modelled and stored as vectors of feature weights or elements. Elements within each vector contribute conjointly to the representation of items. Thus memory representations are not located at specific points within a memory network, or within specific memory systems. Instead they are conceptualised as unique patterns of activation over a common set of elements. Moreover, elements may take on different values in order to represent a variety of different items.

Memory Representations

Memory representations can include items, contexts or, combinations of items and contexts (associations).

1. Items - Items can comprise stimuli, words, or concepts. Each item is modelled as a vector of feature weights. Feature weights are used to specify the degree to which certain features form part of an item. There are 2 possible levels of vector representation for items. These include:
   1. modality specific peripheral representations (e.g., graphemic or phonemic representations of words) (ii)
   2. modality independent central representations (e.g., semantic represenatations of words).
2. Context - Context can be conceptualised as a mental representation (overall holistic picture) of the context in which items, or events have occurred. (e.g., What I ate for "breakfast this morning".) This is also modelled as a vector of feature weights.
3. Associations - Memories are associative by nature and unique representations are created by combining features of items and contexts. Several different types of associations are possible. These can include:
   1. 2-way associations between pairs of items, (e.g., associates - "bacon" x "dog") (e.g., pre-existing associates - "bacon" x "eggs")
   2. 2-way associations between an item and a context, ("bacon" x "breakfast this morning")
   3. 3-way associations between pairs of items and a context ("bacon" x "dog" x "breakfast this morning")

Accessing Memory Representations

Specific cues are required to access the information stored in the distributed memory structure. This type of retrieval is termed cue-based access. Cues can be used to access memory in two ways; via matching or retrieval processes. Test instructions will determine which type of access procedure is used during the recovery phase.

1. Matching - Matching entails the "comparison of the test cue(s) with the information stored in memory" (Humphreys, Bain and Burt, 1989, p.141). This process measures the similarity of the cue(s) and the memory representation. The output of this process is a scalar quantity (i.e., a single numeric value representing the degree or strength of the match). Memory tasks which utilise this access procedure include recognition and familiarity tasks.
2. Retrieval - Retrieval involves the "recovery of qualitative information associated with a cue" (Humphreys, Bain and Burt, 1989, p141). The output of this process is featural information (e.g. an associate of a cue) that can be used to produce a word response. This information is modelled as a vector of feature weights. Retrieval tasks include free recall, cued-recall, and indirect production tasks.

Matching and retrieval processes can also be used to access episodic memory representations or generalised representations.

1. Episodic Access - Episodic access involves the recovery of memories related to specific events. Test instructions are used to cue an episode context (e.g., "What did you eat for breakfast this morning ?"). A representation of the episode context ("breakfast this morning") is then reinstated by the subject in response to the test instructions and used as a cue to retrieve the associated information ("bacon x eggs"). Examples of tasks that access episodic representations include recognition and recall tasks.
2. Generalised Access - Generalised access involves generalised memory representations. Here, subjects do not seek access to specific events or contexts. Instead, they access information which is generalised across a large number of episodes or events. Thus test cues are used singly, without being combined with context cues and responses simply comprise the strongest or set associate(s) of a particular cue. Examples of generalised tasks include production tasks (e.g. Free associate to the word "bacon") and familiarity tasks.

Test instructions will determine which combinations of access procedures are used and what type of information is accessed. By combining different access procedures with different types of information, the Matrix Model is able to account for a wide array of memory tasks.

Summary Table (Humphreys, Bain and Burt, 1989)

Access Process	Process Output	Type of Task
		Episodic	Generalised
Matching	Scalar Quantity	Recognition	Familiarity Rating Lexical Decision
Retrieval	Response Vector	Cued Recall	Free Association Word Completion

Mathematical Model

Symbols

The symbols used in the mathematical model can be summarised as follows:

Words/concepts = A, B etc (uppercase letters, beginning of alphabet)
Context = X
Memory/Vector representations of words and context = a, b, x (lowercase letters)
Items are distinguished by subscripts (e.g. a_i). A distractor item is indicated by a "d".

Vectors

Items and contexts are represented as vectors of feature elements. These elements can assume binary values of either 0 or 1, where 1 is indicative of a feature component and 0 specifies the absence of a feature component. The number of elements in each vector and the proportion of elements assigned a value of 1 are free parameters in the Matrix Model. Although, the proportion of elements assuming a value of 1 will be limited, in order to create sparse representations.

Dot Products

One can measure the similarity of two vectors by calculating the dot (scalar) product of the vectors. The dot product is formed by multiplying a row vector by a column vector.

Example:  Match 

(1 0 0 1) (1 0 0 1)T   = (1 x 1 + 0 x 0 + 0 x 0 + 1 x 1) = 2

Example: No Match 

(1 0 0 1) (0 1 1 0)T  = (1 x 0 + 0 x 1 + 0 x 1 + 1 x 0) = 0

Matches can be performed to compare the similarity between study and test contexts, and the similarity between items encoded at study and test. Matching values are denoted by the following symbols:

c = similarity between the study and test context
s = similarity between the same word encoded at study and test
m = similarity between different words at study and test

>Matrix Products

While individual items and contexts are represented as single vectors (a, b, x), associations between items and contexts are represented by matrices derived from the matrix product of these vectors. Matrix products are formed by multiplying column vectors by row vectors. The resulting matrix product represents the association (or binding) between either items, or item(s) and context. Example 1: 2-way association between a single item (A) and a context (X) This binding is represented as a context-to-item association (xa), where

x = n element column vector
a = n element row vector

The matrix product of this two-way association can be conceptualised as a square and is called a tensor of rank 2.

Example 2: List of items (A₁, A₂,...,A_k) and a context (X) Context and item vectors are multiplied, as above. The resulting context-to-item associations are then summed together in a linear combination and this sum represents the memory of the study list (E).

E = xa₁ + xa₂ + ... + xa_k (1)

Example 3: 3-way associations between a list of word pairs (A₁B₁, A₂B₂,...A_kB_k) and context (X). Each association is represented mathematically as a 3-dimensional array (xa_jb_j), where

x = n element column vector
a_j = n element row vector
b_j = n element orthogonal vector

The matrix products of these associations can be conceptualised as cubes and are known as tensors of rank 3. Rank-3 tensors are produced by postmultiplying the matrix xaj by bj. Thus all of the elements in bj are multiplied with every element in xaj. The resulting associations are then summed together to form the memory for the list (E).

E = 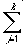xa_jb_j (2)

Pre-existing Memories

Because test performance can be influenced by both list memories and pre-existing memories, list memories (E) are added to pre-existing memories (S), also represented as a n x n matrix (e.g. using Example 3).

M = 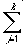xa_jb_j + S (3)

Recognition

Recognition involves a matching process, where the overall similarity between the test cues (x and a_i) and memory (M) is calculated. Because this is an episodic task, the test cues involve both word cues and a context cue (e.g., Did you study these words (A_i), in the list that I showed you before (X) ?). This episodic matching process is accomplished by combining the test cues into an associative matrix (xa_i) and determining a strength value (dot product) between:

(a) the cue matrix (xai), and
(b) the memory matrix (M = 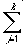xa_j + S).

Example 1: Studied Test Word (A_i)

xa_i . M = xa_i . (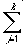 xa_j + S)
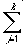= xa_i . xa_j + xa_i . S
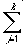= (x . x) (a_i . a_j) + xa_i . S
= (x . x) (a_i . a_i ) + 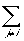(x . x) (a_i . a_j) + xa_i . S

Inserting the expected matching value: E[xa_i.M] = c s + (k - 1) c m + g

where

c = similarity between the study and test context
s = similarity between the same word encoded at study and test
m = similarity between different words at study and test
g = contribution of pre-existing memories

Example 2 : Non studied Test Word (D)

xd . M = xd . (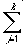 xa_j+ S) (5)
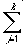= xd . xa_j + xd . S
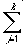= (x . x) (d . a_j) + xd . S

where

E[xd.M] = c m k + g

Note that the matching operations in the above equations can be collapsed down into several components, including :

(a) a match between the test cue and the pre-experimental memories (i.e., xa_i . S or xd . S), and
(b) a match between the test cue and the experimental memories
(i.e., 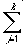xa_i . xa_j or 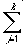xd . xa_j )

The match between the test cue and the experimental memories can further be collapsed down into :

(a) a match between the context on study and test occasions (x . x = c), and
(b) a match between the study and test items (a_i . a_i = s and a_i . a_j = m) or (d . a_j = m)

Thus the final scalar-product derived from these equations, represents the match of the contexts on the study and test occasions (c) weighted by the match of the items on the study and test occasions (s and m). Consequently, memories that are conjointly defined by context and test cues will be weighted more heavily than items not studied in that context. This mechanism enables the model to avoid interference (large weights) from other items studied in the same context and also from previous contexts in which items have appeared.

Cued Recall with a List Associate

This episodic retreival task involves 3-way associations between a list of word pairs (A₁B₁, A₂B₂,...A_kB_k) and context (X). Representations are stored in a rank-3 tensor at study. This is formed by multiplying the matrix xa_j by vector b_j (Refer back to Example 3).

M = 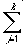xa_jb_j + S

Subjects are then asked to recall list targets (b_i) at test, using list associates (a_i) and context (x) as cues. The retrieval cues (x and a_j) are combined to form an associative matrix cue (xa_i). Retrieval then involves the pre-multiplication of the rank-3 tensor (M) by the retrieval cue (xa_i).

xa_i . M = 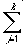xa_i . xa_jb_j + S (6)
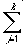= [(xa_i)(xa_j)] b_j + xa_i . S
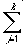= [(x . x) (a_i . a_j)] b_j + xa_i . S
= (x . x) (a_i . a_i)b_i + 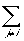(x . x) (a_i . a_j)b_j + xa_i . S

Inserting the expected values:

E[xa_i . M] = c s b_i + c m b_j + g

The end product (matrix product) of this process will comprise a target vector of feature weights. This featural information can be used to produce a word or item reponse.

Note that the target vector is weighted by:

(a) the similarity of the context on the study and test occasions ( x . x = c), and
(b) the similarity of the list cue on the study and test occasions (a_i . a_i = s) and (a_i . a_j = m)

Note also that the weights for the same associate (s) will be greater than the weights for different associates (m). Also, pre-experimental memories (S) are not given a context weight (c). Consequently, context and list cues are able to converge on the appropriate associations. These mechanisms allow the model to decrease interference from other items learned in the same context and also from other pre-existing associates of that cue.

Matrix Model Tutorial Questions

Complete the following questions by accessing the Matrix Model simulator.

1. Run the Matrix Model recognition simulator with the standard parameters and note the d' value (use the prop. figure), the mean familiarity for targets and distractors and the variances for targets and distractors.
2. Simulate a list of 16 items and adjust the criterion appropriately. How does d' change and why?
3. Simulate a list of weak and strong items. How does d' change for the weak items? Why?
4. How would you expect increasing the context strength to affect recognition performance? Conduct simulations to verify your answer.
5. Repeat questions 1-4 for cued recall.

References

Bain, J.D., & Humphreys, M.S. (1989). Instructional reinstatement of context: The forgotten prerequisite. In K. McConkey and A. Bennett (Eds.), Proceedings of the XXIV International Congress of Psychology, Vol. 3. Elsevier, North-Holland.

Humphreys, M.S., Bain, J.D., & Burt, J.S. (1989). Episodically unique and generalized memories: Applications to human and animal amnesics. In S. Lewandowsky, J.C. Dunn & K. Kirsner (Eds.) Implicit Memory: Theoretical Issues. (pp. 139-158). Erlbaum Associates: Hillsdale, N.J.

Humphreys, M.S., Bain, J.D., & Pike, R. (1989). Different ways to cue a coherent memory system: A theory for episodic, semantic and procedural tasks. Psychological Review, 96, 208-233.

Pike, R. (1984). A comparison of convolution and matrix distributed memory systems. Psychological Review, 91, 281-294.

Wiles, J., & Humphreys, M.S. (1993). Using artificial neural networks to model implicit and explicit memory. In P.Graf & M. Masson (Eds.) Implicit Memory: New Directions in Cognition, Development, and Neuropsychology. (pp. 141-166). Erlbaum: Hillsdale, New Jersey.

Note: the type of vector (i.e., row, column, orthogonal) can also be inferred from the order of the vector symbols, where: 1st vector = column vector; 2nd vector = row vector; and 3rd vector = orthogonal.