The Hebbian Learning Rule

Simon Dennis and Rachael Gibson
Special thanks to Jill White

Table of Contents

Vector Exercises

In the following exercises, you will build a vector network that learns to discriminate between stored items and new items (see figure 1).

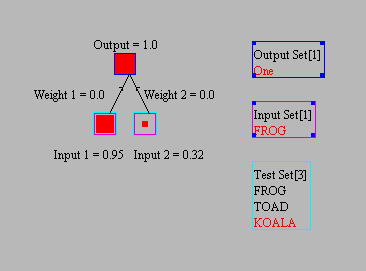
Figure 1: A vector memory network.

Follow the instructions below to create the network and then work through the exercises.

  1. Load BrainWave
  2. Select 'New Hebbian Network'
  3. Set up the vector memory network:
    • Create two input units and one output unit.
    • Connect both input units to the output unit.
    • Set up VALUE objects for the units and weights.
  4. Create the data sets:
    • Create an Input Set containing the two input units
    • Create a Test Set containing the two input units
    • Create an Output Set containing the output unit
    • The items in this exercise are FROG [0.95, 0.32], TOAD [0.49, 0.87], KOALA [0.32, -0.95]. Add the FROG pattern to the input set.
    • Add a pattern containing a 1 to the output set.
    • Add all three items, FROG, TOAD and KOALA, to the test set.
    Exercise 1: Train the network for one epoch and record the weights in the TRAIN FROG row of the following table. How have the weights changed?
    Weight 1 Weight 2
    TRAIN FROG
    TRAIN FROG & KOALA
    TRAIN FROG & TOAD

    Exercise 2: Test each of the items, FROG, TOAD and KOALA, and record the match values (the activation of the output unit) in the second table. Explain the match values.

    TEST FROG TEST TOAD TEST KOALA
    TRAIN FROG
    TRAIN FROG & KOALA
    TRAIN FROG & TOAD

    Exercise 3: Train the network for one more epoch and test again. What happens to the match values after a second training trial? Why?

    Exercise 4: Add KOALA to the input set and an output value of 1 to the output set. Zero the weights (using the ACTIONS menu) and retrain the network on the updated input set. Test the network as before, recording the values in the table in the TRAIN FROG & KOALA row.

    Exercise 5: Delete KOALA from the input set and add TOAD. Zero the weights, retrain and test as above, recording the values in the TRAIN FROG & TOAD row. You should have six weight values and nine match values for each training trial. Create a graph of the match values after the first training trial: plot three lines, one for each test item, against the three training conditions. Explain the shape of each line on the graph.

    Exercise 6: For each of the three training conditions (FROG alone, FROG & KOALA, FROG & TOAD):

    1. Draw the geometric (graphical) representation of the weights,
    2. Provide the algebraic representation of the weights.

    Matrix Exercises

    In the following exercise you will use a matrix memory network to store and recall pairs of items.

    Exercise 7: Load the simulator, BrainWave. From the NETWORKS menu - select Matrix Model (1). What rank tensor does this network implement? What are its dimensions?

    Exercise 8: The items in this exercise are:

    Cues:
    FROG [0.5, -0.5, 0.5, -0.5]
    KOALA [0.5, 0.5, -0.5, -0.5]
    SNAIL [-0.5, 0.5, 0.5, -0.5]
    TOAD [0.5, 0.4, 0.6, 0.45]
    Targets:
    FLIES [0.7, 0.5, 0.5]
    LEAVES [0.7, -0.5, -0.5]
    LETTUCE [0, -0.7, 0.7]
    The input set contains the items FROG, KOALA and SNAIL, paired with items in the output set FLIES, LEAVES and LETTUCE, respectively. Another input item, TOAD [0.5, 0.4, 0.6, 0.45], can be used to test the network on unfamiliar input. Calculate the similarity value (i.e. dot product) of the items FROG, KOALA, SNAIL and TOAD with themselves, and each other, and record the values in the table below:
    FROG KOALA SNAIL TOAD
    FROG
    KOALA
    SNAIL
    TOAD

    Exercise 9: Train the network for one epoch. Test each of the items FROG, KOALA, SNAIL and TOAD. What output is produced in each case? (Give the output pattern and also describe the output patterns in terms of their similarity to FLIES, LEAVES and LETTUCE).

    FROG
    KOALA
    SNAIL
    TOAD

    Exercise 10: Give the algebraic equation that describes the matrix memory formed from the three pairs of associates:

    M =
    Exercise 11: Give the equations that describe each of the retrievals in exercise 9. Use the similarity measures from the table above to simplify each equation to a weighted sum of the target patterns.
    FROG
    KOALA
    SNAIL
    TOAD

    Tensor Exercises

    In these exercises, you will use both rank two and three tensor networks to store and recall triples of items.

    Exercise 12: Load the simulator, BrainWave. From the NETWORKS menu - Matrix Model (2). What rank tensor does this network implement?







    Exercise 13: The items in this exercise are:

    Cues:

    FROG [0.5, -0.5, 0.5, -0.5]
    KOALA [0.5, 0.5, -0.5, -0.5]
    SNAIL [-0.5, 0.5, 0.5, -0.5]
    TOAD [0.5, 0.4, 0.6, 0.45]
    Relations:
    EATS [0.5, -0.5, -0.5, 0.5]
    LIVES-IN [0.5, 0.5, -0.5, -0.5]
    Targets:
    FLIES [0.7, 0.5, 0.5]
    LEAVES [0.7, -0.5, -0.5]
    LETTUCE [0, -0.7, 0.7]
    POND [0.89, 0.43, -0.22]
    TREE [-0.22, 0.76, 0.62]
    SHELL [0.43, -0.5, 0.76]
    Notice that the vectors for the cues are the same as those used above. Also notice that EATS and LIVES-IN are orthogonal to each other - that is they have a dot product of zero.

    Calculate the similarity (dot product) table for the targets.

    FLIES LEAVES LETTUCE POND TREE SHELL
    FLIES
    LEAVES
    LETTUCE
    POND
    TREE
    SHELL

    Exercise 14: The cue+relation input set contains the items FROG-EATS, KOALA-EATS, SNAIL-EATS, FROG-LIVES_IN, KOALA-LIVES_IN and SNAIL-LIVES_IN, paired with items in the output set FLIES, LEAVES, LETTUCE, POND, TREE, and SHELL, respectively. Two other input items, TOAD-EATS and TOAD-LIVES_IN, can be used to test the network's response to unfamiliar input.

    Train the network for one epoch. Test each of the items FROG-EATS, KOALA-EATS, SNAIL-EATS, FROG-LIVES_IN, KOALA-LIVES_IN, SNAIL-LIVES_IN, TOAD-EATS and TOAD-LIVES_IN. What output is produced in each case? (Give the output pattern and also describe the output patterns in terms of their similarity to FLIES, LEAVES, LETTUCE, POND, TREE and SHELL)

    FROG-EATS

    KOALA-EATS

    SNAIL-EATS

    FROG-LIVES_IN

    KOALA-LIVES_IN

    SNAIL-LIVES_IN

    TOAD-EATS

    TOAD-LIVES_IN


    Exercise 15: How does the performance of this network compare with the performance of the network in Exercise 8? Why is it not as good?

    Exercise 16: Give the algebraic equation that describes the matrix memory formed from the three pairs of associates:

    M =

    Exercise 17: Give the equations that describe each of the retrievals from exercise 14. Use the similarity measures from the table above to simplify each equation to a weighted sum of the target patterns.

    FROG-EATS

    KOALA-EATS

    SNAIL-EATS

    FROG-LIVES_IN

    KOALA-LIVES_IN

    SNAIL-LIVES_IN

    TOAD-EATS

    TOAD-LIVES_IN


    Exercise 18: From the NETWORKS menu - select Matrix Model (3). What rank tensor does this network implement?



    Exercise 19: The inputs and outputs for this network are the same as for the previous one, but the connections and hidden SigmaPi units perform different calculations on the inputs to try and achieve the correct outputs. Train the network for one epoch. Test each of the items FROG-EATS, KOALA-EATS, SNAIL-EATS, FROG-LIVES_IN, KOALA-LIVES_IN, SNAIL-LIVES_IN, TOAD-EATS and TOAD-LIVES_IN.

    What output is produced in each case? (Give the output pattern and also describe the output patterns in terms of their similarity to FLIES, LEAVES, LETTUCE, POND, TREE and SHELL).

    FROG-EATS

    KOALA-EATS

    SNAIL-EATS

    FROG-LIVES_IN

    KOALA-LIVES_IN

    SNAIL-LIVES_IN

    TOAD-EATS

    TOAD-LIVES_IN


    Exercise 20: Which of the two networks performs the memory task better? Why?

    Exercise 21: Give the algebraic equation that describes the matrix memory formed from the three pairs of associates:

    M =
    Exercise 22: Give the equations that describe each of the cued recall tests from question 19. Use the similarity measures from the table above to simplify each equation to a weighted sum of the target patterns.
    FROG-EATS

    KOALA-EATS

    SNAIL-EATS

    FROG-LIVES_IN

    KOALA-LIVES_IN

    SNAIL-LIVES_IN

    TOAD-EATS

    TOAD-LIVES_IN


    In this section, we have been looking at the way in which tensors of rank one, two and three can be used to store information.

    Objective Checklist

    The following is a check list of skills and knowledge which you should obtain while working on this chapter. Go through the list and tick off those things you are confident you can do. For any item outstanding, you should refer back to the appropriate section or consult your tutor.
    • understand the distributed representation of items and associations
    • calculate the vector memory values when two patterns are superimposed, in terms of:
      • network weights,
      • Cartesian co-ordinates,
      • vector addition.
    • explain the difference between matching and retrieval tasks and model this difference in the Matrix Model
    • explain the difference between episodic and semantic tasks and model this difference in the Matrix Model

On This Site