Jay Burmeister
Janet Wiles

Departments of Computer Science and Psychology
The University of Queensland, QLD 4072, Australia

Technical Report 339, Department of Computer Science, The University of Queensland, 1995
(This document is - permanently - under construction).
See also: Jay Burmeister�s PhD Thesis (2000)

Table of Contents

1.0 Introduction

2.0 The Game of Go

2.1 Liberties and Capture

2.1.1 Suicide

2.2 Strings

2.3 Eyes

2.3.1 Dead or Alive

2.3.2 False Eyes

2.3.3 Seki

2.4 Repetition of Board Positions - Ko

2.5 Sente and Gote

2.6 Ladders

2.6.1 Snapbacks

2.7 Links

2.8 Groups

2.9 Armies

2.10 Winning the Game

2.11 The Go Handicap and Ranking System

3.0 The Challenge of Programming Go

3.1 A Comparison of Chess and Go

3.2 The Complexity of Go

3.3 Why Go Cannot be Programmed Like Chess

4.0 History of the Computer Go Field

4.1 Academic Work

4.1.1 Zobrist

4.1.2 Ryder

4.1.3 Reitman and Wilcox

4.1.4 Other Academic Work

4.2 Programs

4.2.1 The Many Faces of Go

4.2.1.1 G2

4.2.1.2 Cosmos

4.2.1.3 Many Faces of Go

4.2.2 Go4++

4.2.2.1 Candidate Move Generation

4.2.2.2 Evaluation Function

4.2.2.3 Performance and Timeline

4.2.3 Handtalk

4.3 Computer Go Competitions

4.3.1 The Ing Prize

5.0 What's in a Go Program?

6.0 Performance of Current Programs

6.1 Program versus Program Performance

6.2 Program versus Human Performance

7.0 Future Improvements in Performance

8.0 Go and Computer Go Resources on the Internet

8.1 Computer Go related Internet Resources

8.1.1 Anonymous FTP Archive and Mirror Sites

8.1.2 The Internet Go Server (IGS)

8.1.3 Game Record Formats

8.1.4 The Computer-Go Mailing List

8.1.5 The Computer Go Ladder

8.1.6 Computer Go Competitions/Tournaments and Results

8.1.7 Computer Go Bibliographies

8.1.8 Game Databases

8.2 Go Related Internet Resources

8.2.1 Go Rules and Learning to Play

8.2.2 Go Learning Aids and Tutorials

8.2.3 The Go News Group

8.2.4 The Go Frequently Asked Questions (FAQ)

9.0 Conclusions

Appendix A Common Go Terms and Their English Equivalents

References

1.0 Introduction

This document introduces the reader to the computer Go field and Internet resources pertaining to Go and Computer Go.

For readers unfamiliar with Go, section 2 describes the rules and common concepts of the game. Readers comfortable with their knowledge of Go may skip section 2, reading it only if the use of terms in this document needs clarification.

Section 6 describes the current state-of-the-art in Go programs which is far behind that of Chess programs even allowing for the comparative disparity in the amount of effort expended on developing programs for each game. Theoretical and practical reasons are given in section 3 for this disparity as well as reasons why Go cannot be programmed in a similar fashion to Chess (see Table 1 for a brief comparison).

The history of the computer Go field is briefly outlined in section 4. Included in this outline are descriptions of some of the academic work that has used Go as a vehicle to pursue research, computer Go competitions and results, and programs.

Internet resources pertaining to Go and computer Go are described in section 8. The resources listed include a server for playing a game of Go, an FTP archive site and a mailing list which provides a forum for discussing aspects of programming Go.

2.0 The Game of Go

Go is a two player board game in which chance plays no part. It is an Oriental game which originated between 2500 and 4000 years ago and enjoys a similar status in Japan, China, Taiwan and Korea as Chess does in Western countries.

Go is played on a board which consists of a grid made by the intersection of horizontal and vertical lines. The size of the board is generally 19 x 19, however, 9 x 9 and 13 x 13 sized boards are also used for playing quicker games. Intersection points are connected along the horizontal and vertical lines such that the neighbours of any given point are the intersection points that are horizontally and vertically adjacent to it. Two players alternate in placing black and white stones on the intersection points of the board (including edges and corners of the board) with the black player moving first. The aim of Go is to capture more territory and prisoners than your opponent.

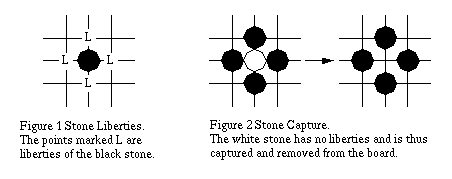
2.1 Liberties and Capture

Empty points that neighbour a stone are called its liberties (points marked L in Figure 1). Any stone which has no liberties is captured and removed from the board (white stone in Figure 2). This is the only instance in which stones, once placed, are moved.

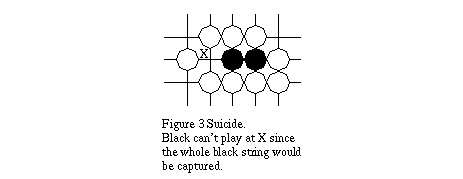
2.1.1 Suicide

A player cannot commit suicide by placing a stone in a position which leads to its immediate capture (points marked X in Figure 3).

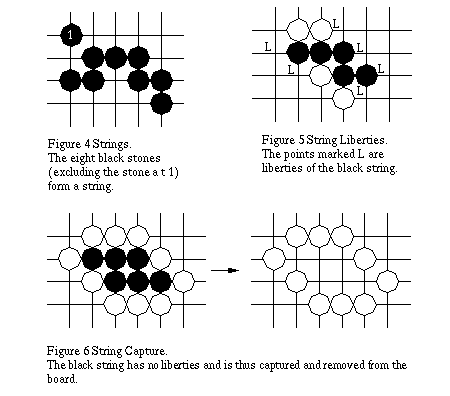
2.2 Strings

Stones of the same colour can be joined into strings by being horizontally or vertically connected to each other (Figure 4). Single stones can also be described as strings which we will refer to as unitary strings. Instead of the stones in a string having individual liberties, the liberties of the constituent stones of the string become the liberties of the string (points marked L in Figure 5). To be captured, a string must be surrounded by opponent stones such that no stone in the string has any liberties (black stones in Figure 6). When a player fills the penultimate liberty of a stone or string, it is courtesy to declare "Atari!" which alerts the owner of the stone or string of its impending capture.

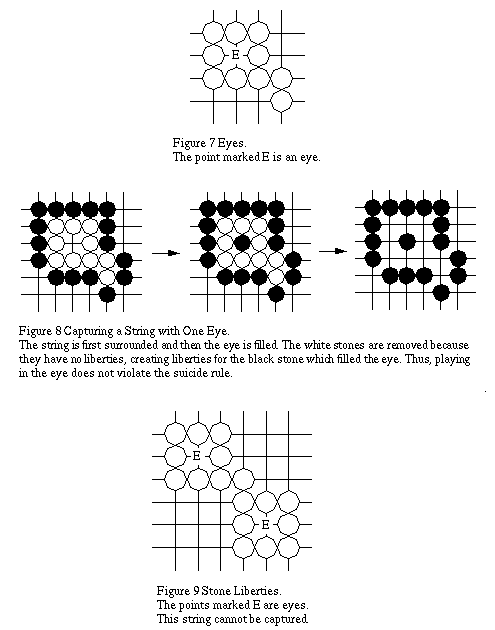
2.3 Eyes

Eyes are formed when a string surrounds one or more empty intersection points (point marked E in Figure 7). Strings which contain a single eye can be captured by first being surrounded and then the eye being filled (Figure 8). Filling the eye does not violate the suicide rule since the opponents captured stones are first removed, creating liberties for the last stone played. A string that has two eyes (points marked E in Figure 9) is safe from capture since there is no way for an opponent to capture such a string. The reason for the inability to capture a string with two eyes is that the stone played in the first eye will be subject to the suicide rule.

Dead or Alive

Strings which have two eyes are said to be alive. In general, a string is alive if it cannot be captured even if the opponent moves first. A string is considered to be dead if there is no way to stop it from being captured even if its owner moves first.

2.3.2 False Eyes

2.3.3 Seki

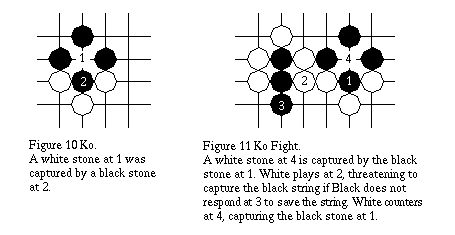
2.4 Repetition of Board Positions - Ko

To stop endless cycles occurring, a player cannot play a stone which causes a previous board position to be repeated. In general, the only situation in which a cycle can arise is called a ko. In Figure 10, a white stone at 1 is captured by a black stone at 2 which could itself be captured by a white stone being played at 1 again. Such a situation is prohibited by the rule against repetition. A ko situation can lead to a ko fight (Figure 11) in which the player which loses a stone in the ko (white stone at 4 captured by black at 1) threatens an opponent stone elsewhere (at 2) and then recaptures the opponent stone in the ko (at 4) after the opponent responds to the threat (at 3).

2.5 Sente and Gote

Skilful players can engineer the game so that they gain the initiative for a number of moves and dictate the response of their opponent. In such a case, a player is said to have sente and the opponent to have gote. Sente usually occurs when players place their opponent in a situation of having to save stones and only having one option available to do so. Sente allows a player to control the course of the game so as to execute a plan of several moves without the opponent being able to frustrate the plan in midstream.

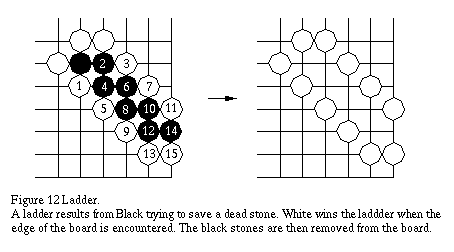
2.6 Ladders

Ladders are a capturing race between a group that is almost enclosed, and a surrounding group. Consider the initial stones in Figure 12 (the stones without numbers). The black stone is doomed to be captured no matter what the Black player does. When White plays at 1, the black stone is threatened with capture. To defend this stone, Black plays at 2. White once again threatens capture by playing at 3. This process continues and results in a ladder being formed. White eventually wins the ladder when the board edge is encountered.

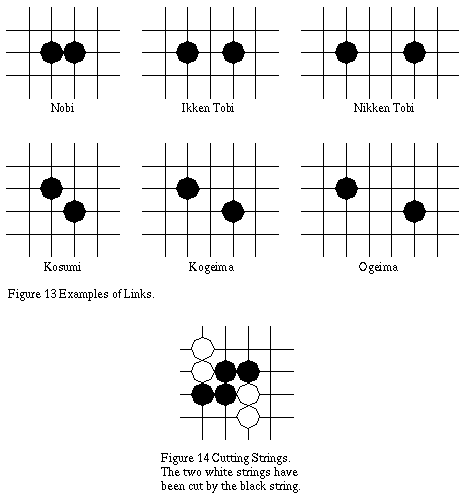
2.7 Links

The only links between stones which is recognized in the rules of Go is between horizontally and vertically adjacent stones (called nobi). In practice however, there are several links which are recognized by experienced Go players (Figure 13). The ikken tobi link can be physically connected as long as black plays next. The kosumi link can be made as long as black plays next or each of the connecting points are empty if white plays first. Of the other links, physical connection depends on the context of the surrounding stones. If two strings are denied a physical connection they are said to be cut (Figure 14).

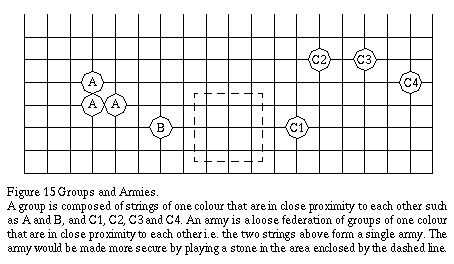
2.8 Groups

A group is composed of strings of one colour that are in close proximity to each other such as A and B, and C1, C2, C3 and C4 in Figure 15. Being in close proximity means that they can be securely linked by one of the links in Figure 13 (other than nobi of course). For the C group, C1 is linked to C2 by an ogeima link; C2 is linked to C3 by an ikken tobi link; and C3 is linked to C4 by a kogeima link. Groups are the main perceptual units concerning the player throughout the game. The most important attributes of a group is whether it is alive, and whether it can create two eyes or connect to a group with two eyes to ensure survival.

2.9 Armies

An army is a loose federation of groups of one colour that are in close proximity to each other. In Figure 15, the two groups (A and B, and C1, C2, C3 and C4) form one army. Being in close proximity means that there are no intervening enemy stings between the groups. Although armies cover a large territory, they are not as secure for defending territory as groups. Thus it is important for a players to convert armies into groups whilst stopping their opponents from doing the same. Converting an army into groups implies playing stones in between strings of separate groups such that they can be linked together as described above (e.g. by playing at one of the points enclosed by the dashed line in Figure 15).

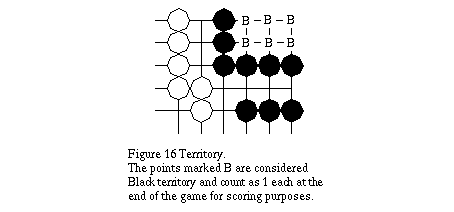
2.10 Winning the Game

A player may pass at any time and the game is over when both players pass consecutively. A determination of territory begins by removing the stones in black strings and white strings which are dead. Each player then adds the number of opponent stones they have captured and the number of empty intersection points which are surrounded by their stones i.e. points that cannot trace a path to an opponent's stone along the horizontal and vertical grid lines (points marked B in Figure 16). The player with the largest territory wins.

2.11 The Go Handicap and Ranking Systems

Go has a sophisticated handicap and ranking system. Players are ranked according to their ability with a complete novice being ranked at 30 kyu (pronounced "cue"). After playing between 10 and 15 games, a player's rank would likely be around 20 kyu. After reaching 1 kyu, further improvement would result in a rank of 1 dan or first-degree master. Amateur ranks continue up to 6 dan. Professional ranks start at what would be 7 dan amateur and extend from 1 dan to 9 dan.

The amount of effort required to increase to the next best rank becomes harder as a player moves up in ranks. For instance, to rise from 20 kyu to 10 kyu would require playing 1 or 2 games a week for around a year and possibly reading a few books on Go tactics and strategy. [The differentiation between professional ranks is also smaller than between amateur ranks. The difference between a 1 dan professional and a 9 dan professional is approximately equivalent to the relative difference of 2 amateur ranks, say 4 dan to 6 dan.] Many years of full-time play is required to reach professional ranking.

To provide balance for both weak and strong players, the weak player is given handicap stones at the start of the game. In the Chinese rules, the handicap stones are placed at the weaker player's discretion whereas in the Japanese rules, the handicap stones are placed on set points called hoshi points. The weaker player is given as many handicap stones as the difference between the players rankings. For instance, a 10 kyu player would give 5 handicap stones to a 15 kyu player. Ranks are usually determined in one of two ways. The first is by finding the number of handicap stones a player needs to win about half the games played against a stronger player on a 19x19 board. The other is by giving 1 handicap stone for each 10 stones that a player is beaten by. The relative value of handicap stones diminish as the board size increases. One handicap stone on a 9x9 board is worth two on a 13x13 board and four on a 19x19 board.

Playing first without handicap is equivalent to a 5 point advantage. It is customary for the weaker player to play first using black stones. If both players are ranked equally, the White player is given a 5 point bonus or komi (pronounced "ko-mee"). In tournaments the komi is usually 5 1/2 points so as to avoid ties.

3.0 The Challenge of Programming Go

Compared to the Chess programming field, the Go programming field is not well developed. A strong commitment to research on programming Chess in the 1960's and 70's has not been replicated in the Go field. There are fundamental differences between Chess and Go which have contributed to making Chess a more attractive research domain so far. However, even allowing for the smaller amount of work done on programming Go, the performance of Go programs have not kept pace with the performance of Chess programs. There are several reasons for this disparity, which is in part due to the complexity of Go and also the unsuitability of the programming techniques used in Chess as described below.

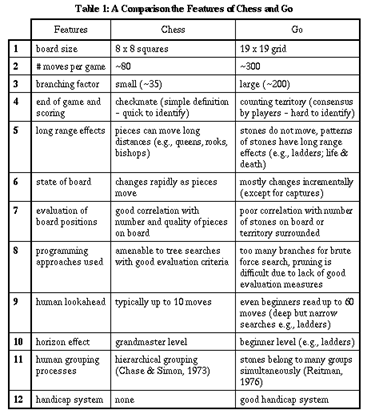
3.1 A Comparison of Chess and Go

1. There are fewer types of pieces in Go than chess (in chess there are 6 types of pieces, whereas in Go each player has only one type, called a stone). However, the board size is much greater in Go (8x8 squares in chess vs 19x19 grid in Go).

2. The size of the board, and the relative freedom in the placement of stones mean that there are also many more moves made in a typical Go game (about 80 moves in chess vs. about 300 moves300 moves in Go).

3. Stones can be placed anywhere on the board, making for a very large branching factor in the selection of each move (estimated at ~200), whereas pieces in chess are constrained to a much smaller set of legal moves (branch factor of ~ 40). The diversity of chess pieces is exploited to reduce the branching factor in chess programs in a way that is not possible in Go (see discussion of evaluation functions in 7. below). The branching factor also plays a role in the different stages of both games (beginning, middle and end). In the opening stage of chess, there are many well-known openings, and these are often followed for up to 10 moves. In Go, the number of sensible openings is much larger, and set openings are rarely followed for more than about 3 moves. However, there are sequences of moves in local skirmishes, known as joseki, that reflect optimal play (for both sides) in tactical battles in the corners. Skill in the use of joseki libraries lies in selecting the right joseki to optimise interactions with stones outside the region of interest or diverge from the known sequence to serve other interests.

4. Both games can be won by resignation of the opponent, or by an outright win - check-mate in chess, or surrounding more territory and taking more prisoners in Go. In chess, the end of a game is easy to determine: checkmate is simply defined in terms of the position and threats to the King. In Go, a game is finished when both players pass, but it is frequently difficult for beginners to know when the end of a game has been reached. Beginners typically prolong play beyond the point where experts would stop, and their difficulties are echoed by Go programs, which also have difficulty estimating when to end a game. The natural end of the game occurs when playing additional stones reduces the player's score, either by filling in their own territory, or giving unnecessary prisoners to the opponent. Go programs are often inefficient in both these ways. There are several different rule systems for scoring in Go: they are all similar, based on calculating the sum of territory surrounded plus prisoners taken during the game for each player, and taking the difference between these scores (a typical margin in a professional game would be less than five points).

5. In both chess and Go, pieces can have long range effects. In chess the effect is directly a result of some pieces' ability to move many squares (e.g, queens, rooks, bishops). In Go, a stone once placed on a grid point does not move (although it can be captured and removed from the board). However, a group (or pattern of stones) does have long range effects in that it can play a role in a capturing race, or can affect the life and death struggle of another group. For example, a stone played in the path of a ladder (a group of stones involved in a certain type of capturing race) can change the potential to link two stones later in the game - even though the stones are on the other side of the board.

6. The state of the board changes rapidly in chess, as pieces move positions. In Go, the board is only gradually changing, as stones are added to the existing configurations. This gradual change compensates significantly for the greater memory load imposed by the larger board. It also allows accurate "read-out" of board positions later in the game - even beginners can read out ladders up to 60 moves ahead (a deep but narrow search). The only time the physical state of the board changes significantly is when a group is captured, and the stones are removed from the board. Groups worth as much as 30 points are often won or lost in a game as trade-offs for other groups, even though the final difference in scores may be just 2 points.

7. Evaluation of board positions (in expert human play) typically reflects both tactical and strategic factors in both chess and Go. However, in chess, there is a good correlation between the likelihood of winning (from any stage of the game) and the number and quality of pieces on each side. Thus in computer chess programs, strategic factors have not been essential in evaluating board position. In Go, there is no strong correlation between winning a tactical struggle over a group, and winning the game, as each tactical struggle over a group requires moves that are not contributing to another group. Early in the game, players strive to achieve influence on the board, rather than directly taking territory. In fact, taking territory at the start of the game can indicate an over-concentrated position, that will not be effective in containing the opponent's territorial moves much later in the game. Algorithmic approaches to measuring the influence of a position are a standard part of most Go programs but there are no methods to confirm their efficacy, except for the strength of the program itself which is usually very weak.

8. For all the reasons discussed above, programming approaches to chess are amenable to tree searches, with good evaluation criteria. Such approaches have not succeeded in Go, because the branching factor is too large for brute force search techniques, and pruning is not a viable option without good evaluation measures.

9. Human lookahead in chess and Go is very different. Beginners of both games might start by only looking ahead a few moves, but in Go, patterns such as ladders can be read out with very little effort, and beginners are soon able to trace the path of a ladder across the board (which can require up to 60 moves). However, in these read-out sequences, there is only one sensible move at each stage, i.e, a series of forcing moves, so there are no alternative paths to follow (see the horizon effect below). In a typical chess game, expert players may search alternative possible moves many steps ahead (although typically about 10), but for each move there are several alternatives. In Go, there are too many alternatives that are reasonable to search far ahead in most moves, although for any move, there are likely to be some sequences that can be very deep (e.g., ladders). This combination of factors is not captured well by either breadth-first or depth-first search techniques.

10. The horizon effect in chess is where a search to a specific depth (such as 12 moves ahead) elicits an evaluation that would be radically altered if a few more moves had been studied. This effect is often seen in sacrifice moves. The horizon effect begins to be a problem at the Grandmaster level in chess. In Go, the horizon effect is seen in assessment of even beginner level play (e.g., ladders).

11. Chess was used in the early 1970s to study human grouping processes, and Chase and Simon (1973) showed that expert chess players view the board in terms of hierarchical groups of stones. In trying to replicate the results with Go players, Reitman (1976) found a completely different structure, in which stones are seen as part of many intersecting groups. Identifying the eventual group to which stones belong is critical in determining their safety, however, from Reitman's research, it appears that no clean assignments can be made until the end stage of the game. Such results indicate sources of potential problems for computer go programs that assign stones into hierarchical groups in order to estimate features such as influence.

12. One major difference in the actual playing of chess and Go lies in the standards of the opponents. In chess, a similar standard is required for an even game. In Go, there is a very effective handicap system, in which a weaker player starts with a predefined number of stones (usually 2-9) placed at influential points on the board. Thus the greater skill of one player is offset by the material advantage of the weaker one. In such contests (and most Go games are of this type) neither player can assume an infallible opponent, for the weaker player tries to simplify the game, and play safely, whereas the stronger player must take more risks, and exploit the weakness of the other player. Although the final score of a Go game is often used as an indication of the relative strengths of the players, the important factor is winning, by however small a margin, rather than taking chances that may increase the margin, but are not as safe. Thus, estimating the other player's level of skill is a critical aspect of many Go games. It is also the case that a Go player needs to be skilled at all facets of the game, rather than having great strength in just one area. This requirement is because players exploit the weaknesses of their opponents. It is common to rank the strength of computer Go programs according to their first game against a human of a given level. In subsequent games, the same human player will often overwhelm the same program that had won previously, because the human will learn the program's weaknesses, but the program does not change.

3.2 The Complexity of Go

An algorithm which can be solved in polynomial time can be practically implemented to solve "real-world" problems. Algorithms which cannot be solved in polynomial time are described as exponential-time algorithms. Except for very small problem spaces, these algorithms are impractical. Problems that can be solved by a computer with a polynomial amount of memory space are said to be solvable in P-space.

It has been shown that, given an arbitrary Go position on an n x n board, determining the winner is P-space hard (Lichtenstein and Sipser, 1980). This result used together with situations arising from ko positions have been used to show that for an arbitrary Go position on an n x n board, deciding whether Black can force a win or deciding on Black's best move is exponential-time complete (Robson, 1983). These results indicate that the use of approximation algorithms which return near-optimal solutions are necessary to solve some aspects of Go and that brute-force search methods will quickly run into difficulties.

A comparison of the complexity of Go to the complexity of other games is provided in Allis et al. (1991). They defined the terms cracked and solved, and illustrated the difference between search-space complexity and decision complexity. A game is said to be cracked if a program is capable of achieving the best possible theoretical results regardless of its opposition. To be solved, the best move must be explicable in human terms. The difference between search-space complexity and decision complexity is illustrated by a variant of Go. The variant consists of players alternatively placing stones on unoccupied points of the board or passing. The first player to place 181 stones wins. This variant has the same search-space complexity as Go, however, since if the player moving first does not pass is bound to win, the decision complexity is trivial.

Allis et al. graphed log log search-space complexity versus log decision complexity, dividing the graph into solvable and unsolvable space for 16 games. Go was shown to be the most complex in both log log search-space complexity and log decision complexity and to be in the unsolvable area. A comparison of Go and Chess shows that 9x9 Go is around about the same complexity as Chess (35 versus 50 in 10 log search space) and that 19x19 Go is a vastly more complex game than Chess and may well be unsolvable as defined above (Allis et al. (1991).

3.3 Why Go Cannot be Programmed Like Chess

Chess programs typically use a heuristic search and evaluation technique. Search trees of board positions are generated to a fixed depth and are heuristically pruned according to an evaluation of the merit of the board positions. This approach works well in Chess because the board size is sufficiently small and the nature of Chess is more tactical than strategic.

Evaluation of a board position in Go presents problems not encountered in Chess. Go is a much more strategic game in comparison to Chess. Unlike Chess, Go does not focus around the capture of a single piece. Positional advantages are slowly built up in achieving the long term goal of acquiring more territory than the opponent. There are many direct and indirect ways to achieve this goal such as making territory, building influence, attacking weak enemy groups, securing friendly groups, destroying enemy territory etc. Due to the large size of the board, a Go game is comprised of many small local skirmishes. If a game of Chess were described as a battle, a game of Go could be described as a war. Many good tactical moves at the local level must all compete for selection in the context of strategic global considerations. Thus a player must balance resources to achieve local goals at many locations whilst trying to pursue an overall global objective.

Due to the problems associated with evaluation, the brute force methods employed in AI to program Chess will not work for Go. As a domain, Go is rich for research in AI and cognitive science. Hans Berliner, a former Correspondence Chess World Champion, a top-ranked U.S. over-the-board player and a well-known Chess programmer referring to Go as saying "... this game may have to replace Chess as the `task par excellence' for AI" (Berliner, 1978).

4.0 History of the Computer Go Field

Early work in programming Go began in the late sixties and was primarily academic in nature. Academic programs are not generally intended to contribute to a general programmable theory of Go, rather they use Go to further other research aims. Serious attempts to develop commercial Go programs was advanced by the spread of personal computers in the home and the financial inducement of the Ing prize.

4.1 Academic Work

4.1.1 Zobrist

The earliest Go program was written by Albert Zobrist as part of a PhD thesis on pattern recognition (Zobrist, 1970). The present description of Zobrist's program will concentrate on those aspects that are relevant to computer Go considerations.

Influence Function

Zobrist introduced the idea of using an influence function to segment the board into black and white territories. The influence function computed a numeric value for every point on the board. Black stones were given a value of +50 and white stones a value of -50 and empty points were given a value of 0. The neighbours of every point that had a positive influence value had +1 added to their influence value and similarly the neighbours of points with negative influence values had -1 added to their influence values. This process was repeated another three times (for a total of four times). This influence function spread black and white influence numerically and Zobrist then segmented the board into areas of contiguous positive and negative numeric values (Figure 17).

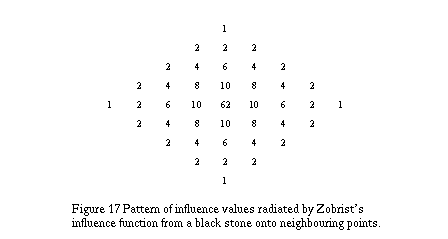
The program constructed an internal representation of the board which was stored as numeric values in various 19x19 arrays. The representation included arrays containing information such as:

• the occupation of a point (black, white, empty),
• number of white and black neighbours, both horizontally, vertically and diagonally,
• the number of stones and liberties for each string,
• the number of empty points adjacent to each empty point, and
• size (including empty points) and number of stones in each segment.

The program also used a second influence function to store an internal representation which measured the influence of stones. It was similar to the influence described above except that occupied points were initially given values of +100 and positive points radiated +3 to their neighbours whilst negative points radiated -4 to their neighbours. Since the computer played black (positive values), this influence function overstated the opponent's influence value so that the program would play cautiously.

Selecting a Move

Having constructed an internal representation, the program performed pattern recognition over the entire board which amounted to searching for certain numeric patterns contained in the program's various arrays. Along with each pattern would be stored an associated move and a numeric value reflecting the priority of the move. When a pattern match was made, the numeric value would be added to the point corresponding to the associated move. An attempt was made to match each pattern "known" to the program across the entire board, rotating and reflecting the patterns as necessary. At the end of this process, the point with the highest value became the program's next move. Thus Zobrist's program used summed feature evaluation to choose its next move.

The program exhibited weaknesses in its play which Zobrist wished to overcome. He divided the game into four phases: corner and edge play at the beginning, extension into the centre of the board, defence and attack of loosely staked out territories, and stabilizing surrounded territories. To enable the program to play appropriate moves during the various phases, only appropriate patterns (along with patterns which were relevant throughout the entire game) were allowed to be matched during those phases.

Results and Improvements

Another addition to the program was limited lookahead or heuristic search. During the pattern recognition process, local areas would be suggested for further examination by lookahead which was carried out to a depth of three moves. The program handled saving/capturing strings, connecting/cutting strings, ladders, and the formation of eyes using lookahead.

The performance of Zobrist's program was modest, beating two novices but performing poorly against experienced players.

4.1.2 Ryder

Jon Ryder's program (Ryder, 1971) can be seen as an extension of Zobrist's approach in as much as it used an influence function and move selection was based on summed feature evaluation. However, Ryder added both strategic and tactical considerations and also used lookahead extensively. The distinction drawn by Ryder between tactics and strategy was that tactical considerations dealt with short-term objectives whilst strategic considerations dealt with long-term objectives

Due to the intractability of using game trees in Go, a suitable replacement had to be found. Ryder's program used the combined analyses of many local tactical problems performed by lookahead together with other analyses as a replacement for the game tree.

Ryder saw Go as a game which required a balance between acquiring actual or potential territory and avoiding the loss of important stones to the opponent. He formulated three areas of interest which were designed to help maintain this balance: board organization showing degree of control of each side over various regions; identification of areas of best play for both sides; and analysis of strings to determine whether they are safe or endangered.

Selecting a Move

Move generation was accomplished in two passes. In the first pass, the tactical status of all strings were determined. Armies, walls and groups were identified and a process of developmental analysis was performed on each which resulted in determining areas and endangered groups for each player. Each legal move was then examined in an attempt to eliminate as many as possible from future consideration with the fifteen best moves being further analysed in the second pass.

The second pass began with an analysis of the best fifteen moves from the first pass with respect to tactical and naive strategic theories. The score obtained by a move from these analyses were added to the score obtained in the developmental analysis. The move with the highest combined score after the first and second passes was then recommended as the next move. Second pass analysis would stop before all fifteen moves were analysed if an "obviously" best move was identified.

Ryder's program used a forward-pruning method to search the game trees that resulted during lookahead. In forward pruning, a decision based on various criteria is made regarding the desirability of pursuing a given branch in a lookahead tree i.e. whether the future implications of a particular move is worth examining. The criteria for terminating a particular search tree included whether a target string had two eyes, whether a saving move resulted in more than five liberties, or it was unlikely that the target would be captured. The danger in forward pruning is that the best move may be discarded before it has been examined.

Influence Function

Like Zobrist, Ryder also used an influence function to provide a numeric number to indicate the degree of tactical control each stone exerted over its neighbours. His influence function was similar to Zobrist's in that black influence was positive and white influence was negative and the influence value at each point was the sum of the influence values propagated by its nearby neighbours. Ryder's influence function was simpler than Zobrist's in that each stone contributed an influence value to its nearby neighbours according to a table of values (Figure 18).

Ryder's influence function.

Both too much and too little influence at a point indicated a problem with playing at that point. Too much influence indicated that there was an over-concentration to the detriment of the global situation whereas too little influence indicated that there was the possibility of capture by the opponent. Optimal moves were those that were close to the peak of the value/influence curve. Influence was regarded by Ryder to be a local property of a stone although he admitted that there were cases (such as ladder-breakers), in which stones exerted control on distant parts of the board. In such situation where the influence value was not a reliable measure, tactical evaluation was used to overcome the short-comings of the influence function.

One situation in which the influence function was not a good measure was that of connectivity. Ryder defined two terms: connectedness and strongly related. The definition for connectedness was that a point was connected to colour X if it was occupied by a non-dead stone of colour X, or if it was empty, it was adjacent to at least one stone of colour X and none of the opposite colour. An extension to connectedness was half-connectedness. An empty point was half-connected to colour X if it was adjacent to at least two stones of colour X and one or more stones of the opposite colour. The definition of strongly related was that a point was strongly related to colour X if it was occupied by or adjacent to a stone of colour X. A point could also be strongly related to colour X if it was diagonally adjacent to a stone of colour X with at least one empty point (kosumi link) or no more than one empty point away (ikken-tobi link). Groups were defined as sets of points which were connected or half-connected.

The influence function was particularly suited to determining walls and armies. Walls were defined as a connected set of points in which the influence values were equal to or larger than a predefined wall threshold. Similarly, armies were defined as a set of points including empty points in which the influence value were equal to or larger than a predefined army threshold.

The tactical concepts employed in Ryder's program included liberty estimation, ko, ladders and snapbacks, and eyes and false eyes. Ryder admitted that improvement was needed in the program's tactical ability which he described as "blunder avoidance".

Representation

Information was included in the representation if it satisfied any of the following criteria: it was basic and was needed in many calculations; it took a significant effort to re-calculate and was used more than once; or it was accessed many times and was constant through many if not all of those accesses.

Groups and armies were represented in a pointer-based manner. There was a pointer from each point in a group or an army to the entity descriptor of the group or army it belonged to. Each entity had a pointer to one of the points that comprised it which was the base point for that entity. Searches for points near entities were initiated from the base point.

The global representation of the board was contained in a 21x21 array (19x19 with an empty point border around the outside). By using various bits in the memory location of each point in the array, the following information/pointers were able to be stored: area number; army number; wall number; group number; string number; and current state (black, white or empty).

Results and Improvements

Ryder reported the results of only one game which was lost to a novice which had just learned the rules and had been given some rudimentary tips on the tactics and strategies of Go. With regard to Ryder's main interest, he reported that the tactical analysis was quite an efficient searching mechanism which provided valuable information for move generation and compared favourably to the powers of analysis exhibited by human beginners. He was also of the opinion that only a small effort would be required to improve the program's tactical strength.

Future improvements suggested by Ryder included re-using previously calculated information in searching, the incorporation of distant ladder-breakers into tactical analysis and improving the definition of endangered groups. Ryder identified the developmental analysis stage which consumed around 10% of the processing time as needing attention. One possible reason for the poor performance of Ryder's program was that it made no distinction between the opening, mid and end games and was therefore playing inappropriate tactical moves in the end game in particular. The addition of such distinction was recognized to be of importance in future improvements by Ryder.

4.1.3 Reitman and Wilcox

Walter Reitman and Bruce Wilcox began using Go to conduct research in 1972. The program that resulted from that research has been described both as the Reitman-Wilcox Go program and to the INTERIM.2 Go program. After the research project was discontinued, Wilcox rewrote the INTERIM.2 program to produce NEMESIS, a commercial Go program.

The research conducted by Reitman and Wilcox using Go was predominately in the Artificial Intelligence area and included pattern recognition (Reitman et al., 1978; Reitman and Wilcox, 1975,1978), planning (Reitman and Wilcox, 1974) and replication of human perceptual and cognitive abilities in Go. Indeed, the objective of program was to model human go play and to this end, they videotaped protocols and post-game analyses of a strong Go player to try to ascertain how humans play Go.

According to Reitman and Wilcox, the three essential ingredients to a Go program are perception, knowledge and coordination (Wilcox, 1988). They tried to incorporate into their programs representation as many of the perceptions of a skilled Go player as they could. They identified and stored two types of Go knowledge: process knowledge which included how to kill a group, how to make territory, etc, and evaluation knowledge which enabled the stability of groups etc. to be judged, the estimation of relative values, etc. Coordination of the program's perceptions and knowledge was achieved through appropriate control structures which allowed it to choose the next move.

The INTERIM.2 program created and maintained a representation that was a selectively updated, multilevel network which Reitman and Wilcox said was analogous to the type of perceptual and cognitive representation a skilled Go player would create. There was a hierarchy of experts and critics which operated on the network which chose the next move. Lookahead was not full-board, rather it was a selective, goal-driven process.

The INTERIM.2 Program

INTERIM.2 summarized information up and filtered decisions down (Wilcox, 1988). Information contained in low-level representations e.g. strings, were summarized and used in high-level representations e.g. groups. The program made decisions at a high-level about what to "focus on". These decisions were filtered down to lower levels and influenced decisions made at those levels.

Flow of Control

The program stored its representation in a structure called GAMEMAP which was indexed through a set of interrelated arrays called GAMEBOARDS. In each GAMEBOARD array there were pointers that pointed to every instance of a particular data structure e.g. STRING-BOARD contained pointers to every string on the board. The GAMEBOARDS progressed from simple to complex: TYPEBOARD, STRINGBOARD, LINKBOARD. Special GAME-BOARDS such as LENSBOARD, WEBBOARD, SECTORBOARD and TACTICSBOARD were designed to contain representations which corresponded to a skilled human players perceptual and cognitive representations.

The flow of control in the INTERIM.2 program oscillated between MOVE and REFLEX. MOVE selectively updated the components of GAMEMAP that were affected when stones, black or white, were placed on the board. REFLEX was responsible for choosing the program's next move which was achieved by stepping through an ordered list of functions and accepting the first move returned by them.

The Tactician (PROBE)

The program's tactician, PROBE, was used to answer specific questions and therefore performed narrow, goal-driven lookahead instead of general purpose, full-board lookahead that is common in Chess programs. The basic assumption behind PROBE was that if the results of a small number of intelligently chosen lines were the same for a given question, then those results would most likely be the answer to that question. Such an assumption is not always valid, however, Reitman and Wilcox felt it was a small price to pay for a quick searching and was not dissimilar to the penalties experienced when human searches failed for similar reasons. PROBE was designed to model how skilled human Go players performed tactical problem solving by selective lookahead (Reitman and Wilcox, 1979).

PROBE would be employed to answer a specific question and would propose a reasonable initial move.The initial move would be hypothetically played and a new hypothetical board position would result. PROBE would then propose another reasonable move based on the hypothetical board position. This would continue until a position was reached which could be judged as either a success or a failure with respect to the specific question that PROBE was trying to answer. If the position was a success, PROBE returned the initial move as the result. If the position was a failure, the hypothetical moves were retracted until there was a position in which a reasonable alternative move could be made and the process was repeated. In unrestricted lookahead, all moves were examined in this fashion so that the best move could be discovered. In PROBE, not even all reasonable moves were examined. Each side was limited to two or three failed variations before the search was terminated and a failure result was returned.

The selection and examination of reasonable moves was conducted by a hierarchy of experts which formed, evaluated and implemented goal-directed "chains of thought" (Wilcox, 1988). There were a variety of experts including experts that generated goals and subgoals, experts that proposed moves to realize goals, experts that used exclusively the current board position and current goals, and experts that used all goals and subgoals. The experts contained a large amount of specific Go knowledge. The control structures implemented by Reitman and Wilcox in PROBE allowed the knowledge contained in the various experts to be organized, easily debugged, and readily extended (Wilcox, 1988). The goal-directed behaviour of PROBE resulted in very restrictive searching which typically resulted in around 60 - 80 hypothetical moves per lookahead (Wilcox, 1988).

Perceptions and Representations

INTERIM.2 maintained many different data structures in its representation. Point occupancy (black, white, empty) was used to determine strings. A basic property of each string was whether it could be captured or saved. The links recognized by INTERIM.2 were kosumi, ikken-tobi, nikken-tobi, kogeima and ogeima. Links were classified as normal (connectable), dead (unconnectable but potentially useful) or string capture (linkages between strings capturing an opponent string). Basic properties of linkages included whether they could be joined or cut, whether they crossed opponent links, and why they were created. Special edge linkages which were links from strings up to the fourth line to the edge of the board were also recognized. Sector lines were long range links and were used in stability assessment and move generation. Virtual strings were strings connected by unbreakable links. Groups were sets of strings joined together by links. Enclosed territory was a set of empty points or dead stones that were enclosed by strings, linkages and edge linkages.The motivation for moves e.g. why a link was created, was explicitly tracked to facilitate move selection and to ease debugging.

Influence was radiated using Ryder's algorithm. Reitman and Wilcox saw influence as misleading in certain situations and therefore developed the notion of influence blocks. Areas of empty, contiguous, same-signed influence points that did not include linkage points were collected into a structure. The perimeter of these structures were located and then iteratively "shrunk" to provide nested loops. Since shrinking did not take place across stones or linkage points, it was possible that the loops created in the shrinking process would become arc segments or strips. Eventually individual structures emerged which were called influence blocks. Points contained in an influence block were considered more likely to be turned into territory the further they were away from the perimeter of the block.

Creating and maintaining INTERIM.2's representation was described by Reitman and Wilcox as perception and the data structures used were also sometimes referred to as perceptual representations.Two components of the perception system employed by the INTERIM.2 program are particularly interesting. Webs were used to determine what regions could be "seen" from a stone and lenses were used to monitor actual patterns of stones in a game using the program's knowledge of Go patterns.

A web was constructed around a group as concentric "circles" of liberty points (circumferential strands) to a maximum depth of nine levels. Radial strands emanated from the groups. The web did not continue behind other stones, either friendly or unfriendly. Links between stones and between stones and the edge of the board (up to three moves away) also stopped a web. The continuous loop of the outermost points of a web comprised its perimeter. The points between the group and the perimeter were considered to be transparent. The perimeter of a web was useful information for a group in deciding where potential threats might come from, where it could run to avoid those threats, the location of nearby friendly groups, where linkages might be attacked etc.

To Reitman and Wilcox, local stone configurations and their transformation by sequences of moves is a fundamental aspect of Go. Sequences of moves associated with standard configurations e.g. attacking or defending a kogeima link, are recognized by competent Go players. Lenses were designed to monitor such configurations and suggest moves that were known pattern continuations.

A lens was comprised of a set of fields. Each field consists of a set of points and watches for the development of a sequence of moves. The lens in turn supplied information about the suggested moves and global status information to the tactician. When a field recognized a configuration, it supplied suggested moves and other associated information to the lens. When fields no longer recognized patterns they were discarded which caused a lens to get smaller over time. This in effect amounted to the "focus" of a lens becoming more concentrated over time.

Performance

The results of three games played by the INTERIM.2 program are reported in Reitman & Wilcox (1978). Two were won against players ranked 22 and 34 kyu and one was lost against a player ranked 4 kyu. The computed ranking of the INTERIM.2 program from these games was 27 kyu.

Reitman and Wilcox were pleased with the performance of the INTERIM.2 program in regard to their initial objectives of modelling human play. It played conservatively, choosing to defend endangered groups in preference to attacking opponent groups. It defended well; the only cases in which it lost groups (other than due to bugs) were when several groups were simultaneously endangered.

4.1.4 Other Academic Work

Some of the academic work that has used Go as a domain is presented below. The various papers are described at a high level since, in general, they do not provide specific details that would be of use in developing a Go program.

Lehner

Paul Lehner, a student of Wilcox, produced a PhD on strategic planning in Go (Lehner, 1981) which is also described in Lehner (1981). His work was based on representative search which Wilcox found to be frequently exhibited by Go players (Kerwin and Wilcox, 1973).

A representative search provides information about many potential move sequences that satisfy a strategic plan by examining only one of those sequences. Lehner's results suggested that representative lookahead was not alone sufficient to evaluate strategic plans, however, it could quickly reject strategically unsatisfactory plans. He saw the use of representative search as providing a means to reduce the number of moves that would be passed on to a more precise tactical lookahead mechanism.

Stoutamire

Go was used as a domain for researching machine learning by David Stoutamire (1991). A simple error function was developed which, rather than incorporating tactical or strategic Go knowledge, was derived from a database of expert games. Stoutamire then developed a classification technique called pattern preference which automated the process of deriving patterns that were representative of good moves. Due to exponential growth of the pattern database, a hashing function was developed which had the nice property of graceful degradation as memory requirements increased.

Sander

To avoid the combinatorial explosion that results from using tree search to evaluate and select moves, Peter Sander (1979) devised a program with a top-down or goal directed organization that used strategies to generate possible moves. Sander's program (called Kyu) generated bottom-up hierarchically structured descriptions of board positions which were incrementally updated after every move. It progressively refined its strategies into goals and then selected moves. Kyu only played the opening game to move 25 and an intended look-ahead mechanism was also not implemented.

Kyu's data structures were based on linked records which represented strings, groups and armies of both colours. From any point on the board, it was possible to access the string, group and army that the point belonged to if occupied, or had influence over it if unoccupied, by following pointers. After each move, the data structures were incrementally updated to reflect the changes caused by a move. The update was from low-level to high-level: from points to strings, from strings to groups, and from groups to armies.

The architecture which was instantiated in Kyu was summarized by Sander as being comprised of a multi-level structured data representation, and a hierarchically organized planning system which explicitly encoded strategies and goals. He also believed that such an architecture had applications in different domains other than Go.

Friedenbach

Kenneth Friedenbach studied the interaction of perception and cognition in the solution of complex problems by using Go as a domain (Friedenbach, 1988). He formalized the notion of abstraction hierarchies which are based on graph theory and then applied them to Go. The use of Go as a domain was because, according to Friedenbach, concepts in the Go literature are related in a multi-level hierarchy.

Friedenbach's model of perception and cognition involved three components. The first was a hierarchy of static objects which consisted of five levels: the points of the board, strings of similar points, groups of related strings, loose federations of groups or potential groups (armies), and a summary of the properties of the federations in a global level. The second was an analytic component concerned with changes in structures as a result of sequences of moves or transformations that are considered. The third was an integration component concerned with the retention and application of information from one analyses to another.

Four types of analysis were carried out. Tactical Safety analysis was carried out at the string level and was concerned with capturing and protecting strings. Strategic Safety analysis was concerned with killing and defending groups and involved analysing eyes and connections. Strategic Development analysis was carried out at the group level and was concerned with open areas, balance measures, the growth of new groups, and the interactions of emerging groups. Global Balance analysis was the highest level of analysis and was concerned with initiative and the overall strategy of the game.

Friedenbach characterizes an analysis by three conditions: the condition under which it is performed, the conditions under which it is terminated, causing its evaluation, and the conditions under which continuations are chosen. Friedenbach uses tactical analysis as an example. Tactical analysis is invoked whenever there is a string that has less than three liberties and is terminated when all strings have three or more liberties. Continuation involves considering atari moves and captures by the attacker, and captures or liberty increasing moves by the defender. A reanalysis would result if a move was made which affected the number of liberties of a key string during the analysis.

4.2 Programs

A description of past and present Go programs are given for those programs that such details could be obtained. Other programs are listed together with their programmer(s) without description in the results in section 6.

4.2.1 The Many Faces of Go

The Many Faces of Go (MFG) is one of the best commercial Go programs currently available. David Fotland has been writing Go programs on a part time basis since 1981 and released MFG in 1990. Fotland has continued to enhance MFG since then and has contributed regularly to discussions on the computer-go mailing list concerning computer go programming in general and MFG in particular. MFG evolved from two other significant programs: G2 and Cosmos.

4.2.1.1 G2

Fotland's first Go program determined territory by radiating influence. Unfortunately, it could be beaten by a simple liberty filling algorithm so he discarded it and wrote G2. The internal structure of G2 was described by Fotland in terms of its data structures, its tactical analyser, and its move selector (Fotland, 1986). G2 used full board reading and evaluated all legal moves with an emphasis on strategic moves. After the full board evaluation of all moves, the move that received the highest score was played.

The Data Structures

Most of G2's code was devoted to updating the data structures. Stones occupied points (referred to as squares) and were organized into strings (referred to as groups) and then into groups (referred to as armies). Data was associated with each point on the board and included the distance to the nearest and second nearest edge, a list of adjacent and diagonal neighbours, string number of the stone occupying the point, the number and a list of liberties, colour of stones on neighbouring points (white, black, or mixed), an influence function, and the nearest occupied point in each direction.

Horizontally or vertically adjacent points containing like-coloured stones were organised into strings. String data included colour, number and list of liberties, a list of its connections, a list of neighbouring enemy strings, the army it was part of, and an aliveness value (described below).

The types of connections recognized by G2 included one and two point jumps, diagonal connection and knight's move. Connection data included the strings it joined, its type, the points involved, and its status.

Groups were comprised of strings which were connected by unbreakable connections or were both adjacent to a dead enemy string. Group data included a list of its constituent strings and dead enemy strings used as connections, the number of stones and liberties, the number of eyes, and an aliveness value.

The Tactical Analyser

The tactical analyser was used to evaluate board positions so that a move could be selected. Each group was assigned an aliveness value which was also inherited by its constituent strings. The strength of G2 was primarily determined by the tactical analyser and consumed the largest portion of Fotland's effort (Fotland 1986). Since most of the program's time was spent in the tactical analyser, it had to be both fast and efficient in its pruning of search trees.

Aliveness values resulted from a multi-stage process: strings which could be captured were identified as dead; eyes were found by the eye evaluator; unbreakable connection were identified; connected strings were identified as groups; territory was determined by the territory evaluator; and the life and death evaluator assigned an aliveness value to each group which was then assigned to its constituent strings.

The tactical analyser examined every string with less than five liberties to determine whether it was dead i.e., whether it could be captured; strings which could obtain at least five liberties were assumed to avoid capture. Interesting moves were suggested during lookahead to determine the status of a string. Interesting attacking moves included geta moves for groups with two liberties, liberty filling moves, moves adjacent to an enemy string's liberties, and liberty gaining moves for friendly strings. Interesting defensive moves included diagonal moves into unoccupied territory, one point jumps, extensions, connections, and liberty filling moves (for adjacent enemy strings).

The interesting moves were heuristically evaluated and the best were selected for further analysis. The best of these moves was hypothetically played and the resulting situation analysed from the opponents point of view. Once again, the best moves were chosen and the best one was hypothetically played. Normal backtracking was used at each stage as well as alpha-beta pruning. Thus, a depth-first tree was generated until the string being examined was captured or gained sufficient liberties to live. The search tree was generated to a maximum of 80 moves which still enabled ladders to be accurately read. The number of "best moves" considered (between 1 and 3) depended on the depth of the current move in the search tree: more moves were considered near the root and less near the leaves. Since the value of the terminal node had only two values (i.e., captured or escaped), alpha-beta pruning was very efficient (Fotland, 1996).

An eye evaluator was used to maintain information about eyes, half eyes (eyes made in gote) and quarter eyes (eyes needing two moves to be made) by evaluating small enclosed eyespace. G2 recognised some basic dead shapes and various types of eyes including three in a row, four in a square, bulky five, pyramid, and cross.

Groups were determined by finding strings that were connected by unbreakable connections. The tactical analyser tried to cut connections to test their strength. Dead opponent strings could also be used as connections between live friendly strings.

Territory was determined by the territory evaluator. As well as completely enclosed territory, G2 also evaluated territory near the board edge which did not need to be completely enclosed. Territory could be made near the edge by being between a stone and the edge or a connection and the edge. However, such territory could be challenged by a stone within four lines along the edge, and closer to the edge (undercutting the edge).

The life and death evaluator analysed every group. An aliveness value was assigned to each group by considering the number of liberties it had, its eyespace, the amount of territory it controlled, whether it could extend along the edge, its size, whether it was in contact with an enemy string, and whether it was completely surrounded. The aliveness value rating itself had 20 different values including "has two eyes", "has enough space to make two eyes", "unsettled", "not enough eyespace", and "can't possibly make two eyes".

The Move Selector

A rule-based strategic evaluator with 65 rules was used to select moves by choosing the highest scoring move using a two step process. In the first step, strategic moves were evaluated and in the second step, all legal moves were evaluated. Information from the data structures and the tactical analyser was used to evaluate board positions resulting from moves in both step one and two. Fotland felt that this was the weakest component of G2 due to the weakness of the data structures (Fotland, 1986).

The rules suggested strategic moves to evaluate such as playing in an empty corner, make shimari or kakari, a move from the joseki dictionary, extending along an edge, invasions, contact fights, blocking, cutting, connecting, blocking an invasion on a wall, or making a ko threat.

In the first step, all the suggested strategic moves were evaluated. A particular strategic move was hypothetically played and the resulting board position was evaluated. The evaluation process consisted of assigning values to the board points and then summing them together to return an overall score. The value for a given board point was determined by the aliveness value of the string that controlled it. If the board position resulting from a strategic move did not satisfy the strategic goals associated with the rule that suggested it, the evaluation of the move was ignored.

In the second step, all legal moves (including the strategic moves considered in the first step) were evaluated. The value assigned to a board position resulting from hypothetically playing a move was based on the aliveness, size, and amount of territory controlled by each string on the board.

The values that resulted for each move from step two were summed with the value they obtained if they were considered in step one. The move with the overall highest score was then chosen as G2's next move.

Size, Performance and Timeline

Between 1981 and 1988, Fotland spent around four years part time writing G2. He stopped work on G2 for several years because the available computers were not fast enough for the development of strong Go programs (Fotland, 1996). G2 was around 11000 lines of C code and used around 700k for the code and data. During that time, Fotland's Go skill advanced from 15 kyu to 1 dan. G2 played at about the 25 - 20 kyu level and could beat beginners without much trouble (Fotland, 1986). Fotland had some success at computer Go competitions with G2 coming 4th in the world computer Go competition in Taiwan and 1st in the US computer Go championship in 1987.

4.2.1.2 Cosmos

Fotland converted G2 into Cosmos in 1988. The main difference between Cosmos and G2 was that instead of evaluating all legal moves, only suggested moves were evaluated. This transition was achieved by increasing the number of move suggestors to over 250. Quiescent search was added and the connection, eye, and territory evaluations were made more accurate (Fotland, 1996).

Data Structures

The data structures used in Comos were basically the same as those used in G2. The eye information included the number of eyes achievable in gote, the number of eyes achievable in sente, the number of eyes achievable if the opponent moved twice, a list of vital points, and eye type. The information contained in the data structures was updated either incrementally (e.g., lists of liberties) or after every move (e.g., influence).

Tactician

Essentially, Cosmos had the same tactician as G2 but better move generation and sorting. In Cosmos, the tactician was only used to determine dead and threatened strings by trying to capture them. Its parameters were maximum liberty count, maximum, depth, and maximum search size. The maximum liberty count was 4, and therefore as for G2, strings with more than 4 liberties were assumed to avoid capture.The maximum depth allowed was 100. The search size determined the playing level (Stoutamire, 1991) and since forcing moves were not counted, ladders could be accurately read even at low playing levels.

Influence Function

Territory was determined by radiating positive influence from alive groups and negative influence from dead groups. Radiated influence did not pass through stones or connections and was inversely proportional to distance.

Board Evaluation

Life and death of groups was the primary concern dealt with by the evaluation process. Board positions were evaluated by a similar process to that used in G2 with the addition of quiescent search.

The tactician was used to determine dead and threatened strings (those that could be captured if they moved second) and whether the stones at the diagonal of eyes could be captured. This information was useful in identifying unbreakable connections and forming strings into groups.

Eyes were analysed to determine their potential and then allocated to groups. False eyes were identified by checking the diagonals of eyes and some dead shapes were also known by Cosmos. Any group with enough eyespace to make two eyes was considered to be alive. Potential eye space could be gained by extensions along the edge, possible connections, being adjacent to a threatened enemy group, and by controlling territory which was not already considered to be an eye.

There were 25 values that described a groups strength in terms of its life and death status. The values were divided into five main categories which included very alive, alive, unsettled, weak and dead. Determining the strength of a group included considering potential connections, potential eyes, and potential extensions along the edge. Positive influence was radiated from alive groups and negative influence was radiated from dead groups with black and white influence being maintained separately.

Weak groups which were contacted by the influence from friendly alive groups were considered not to be surrounded. Weak groups were further divided into those that could run and fight and those which would almost certainly die.

In general, board points were scored according to the radiated influence values. However, occupied board points, board points adjacent to a stone and board points between a stone and an edge were scored differently. Unsettled groups were scored according to who as to play next.

Move Selection

Cosmos had over 250 rules that suggested moves which included fuseki moves (including shimari, kakari and joseki moves), edge moves, playing in the centre, playing safe when ahead of opponent, "squirming" around when behind opponent, pattern matching, saving weak friendly groups (including making eyes, running, or fighting semeais), killing weak enemy groups, cutting, connecting, contact fights, ko threats, and filling dame. Cosmos had a joseki library which contained around 5000 suggested joseki moves and a pattern database which had 60 patterns which were 5 x 5 in size. Whenever a match was made, the rule (code) associated with the pattern was applied (executed) and would then suggest a move. The addition of extra moves to be suggested could easily be accomplished by the addition of new move suggestor rules or the addition of patterns.

The rules would supply a guess value (probable evaluation of the move), bonus value, minimum aliveness value, and would indicate which groups were being attacked or defended if any. The moves were sorted by their guess values and, depending on playing level, a certain number were "played". Moves could be rejected before being evaluated if they did not "apply". A move applied if it accomplished what it was intended to do: if a move was intended to defend a group and the group ended up weaker than it started the move was rejected. Surviving moves were awarded a sente bonus if they achieved sente. The position resulting from the move was then evaluated. The evaluation score, the sente bonus and the rule bonus were summed together and the highest scoring move was selected as the next move.

Size, Performance and Timeline

It took Fotland nine months to compress G2 down to 512 k and add a new user interface. In 1988 Cosmos was released by Ishi Press for IBM-PC as Cosmos, The Computer Go Partner and was released a second time in 1989. Due to the amount of time spent on the user interface, Fotland was unable to devote sufficient time to improving Cosmos' playing level and its performance in various world computer Go championships was modest coming 8th in 1988 and 7th in 1989 (Fotland, 1996).

4.2.1.3 Many Faces of Go

After a rewrite of the user interface and addition of professional graphics and new features, Cosmos was released as The Many Faces of Go in 1990. Additions to MFG included a limited full board lookahead capability, consideration of the value of sente, and a strategy function which is used to focus attention on the important areas of the board and to identify urgent moves. The number of patterns in both the joseki and pattern databases were increased. The pattern database was also improved by increasing the pattern size from 5x5 to 8x8, by storing many suggested moves for each pattern in a move tree (rather than just one per pattern as for Cosmos), and by a complete rewrite which encompassed algorithms, code, and data structures and lead to an increase in speed (Fotland, 1996).

Data Structures

The dynamic data describing a board position is stored in three classes of data structures: incremental, locally recalculated, and globally recalculated. The data in the incremental data structures is updated upon addition or removal of a stone and includes low level information such as lists of empty points, number of liberties etc. Locally recalculated data is updated as it is needed i.e., it is only updated for regions of the board which have been affected by a particular move or move sequence, and includes connection strength, and eyes. Globally recalculated data is updated for the whole board and includes group strength and influence. The locally and globally recalculated data structures are maintained by the evaluation function.

The dynamic data is stored globally and is generated progressively in several passes of increasing abstraction. The dynamic data used in MFG includes point environment, string data, connection data, eye data, potential eye data, group data, territory, and score.

An instance of the connection data structure stores information pertaining to connectivity between two strings. Each connection has a list connection points i.e., a liberty of one string which is no more than three points away from the other string. Thus, the connection recognised by MFG include hane, one point jump (ikken tobi), knights move (kogeima), two point jump (nikken tobi), large knights move (ogeima), three point jump, and bent three point. Other special connections near the board edge are handled through the pattern database. The data stored in the connection data structure includes the strings involved in the connection(s), the number of and lists of one, two and three point connections (i.e., as measured from the connection points), the type of each connection, and the strength of each connection (e.g., already cut, cuttable, shared connection, connected with aji, connected solidly). Other than the type and strength data which is stored in a locally recalculated data structure, the connection data is stored in an incremental data structure.

The eye data structure records information pertaining to either a block of empty point or dead enemy strings which are partially or completely enclosed by friendly stones. Data stored in the eye data structure includes colour, a list of the points in the eye, vital points, and eye type (e.g., one point, two point, line eye, big eye, and dead group eye). The number of eyes (to a resolution of 1/8 of an eye) achievable under various conditions were recorded including the number of eyes if opponent moves twice, number of eyes if opponent moves next, and number of eyes if program moves next. A board point can only be recorded as belonging to one eye. The eye data structure is a locally recalculated data structure since eye data does not lend itself to incremental update. In hindsight, Fotland says that a pattern based approach to recognizing eyes would be preferable (Fotland, 1993).

The evaluation of group strength and the generation of attacking and defending moves involves identifying potential eye space and running points. The potential eye data structure contains type, value and location data for potential eyes. An examples of data stored in the potential eye data structure is "extend along edge" (type), value is number of new points of eye space, and location is the liberty to extend from. Running points are stored by type (e.g., running towards friendly/unfriendly stones) in several different lists. Potential eyes and running points are stored in a globally recalculated data structure.

Tactician

Every string with three or less liberties and many strings with four liberties are read by the tactician. Each string is read twice, once with White moving first and once with Black moving first. The tactician determines whether a string is captured (i.e., can not live even if it moves first), threatened (i.e., it lives if it moves first and dies if it moves second), or stable (i.e., lives regardless of who moves next). The tactician relies on simple heuristics concerned with the number of liberties and connectivity; pattern matching is not used in the tactician.

The tactician has two separate move generators; one to generate attacking moves and one to generate defensive moves. The moves suggested by the move generators are sorted according to criteria which include second order liberties, cut points, and simple eye shapes. Once sorted, an alpha-beta depth-first search is employed with the performance of the search depending on the quality of the move sorting (Fotland, cgm1 5 Mar. 1993).

Tactical searches are goal directed and are limited to a maximum number of nodes. For string captures this is around 100, however, when only one move is suggested, it is not counted towards the node limit. In this way, ladders can be read without problems (Fotland, cgm1 14 Oct. 1993). The number of nodes for a search are allocated to the branches according to the value given to the moves by the first ply move generator and thus different branches may end at different depths. The branching factor at each successive ply is progressively constrained by the tactician. The branching factor falls from five at the first ply to one or two by the fifth ply.

Since the data structures in MFG are separated into incremental, locally recalculated and globally recalculated, low level local tactical searches can be executed quickly by only updating the incremental data structures. However, the possible goals of such a search are limited since the high level data structures are not recalculated. It is not possible, for example, for MFG to search for x liberties and two eyes (Fotland, cgm1 3 Nov. 1993).

The tactician is used to read connections and eyes. A cutting stone can be examined by the tactician to determine whether or not it will be captured. Stones on the diagonal of eyes can be examined to determine whether they can be captured. These types of search do not exceed around 12 ply since the program actually plays worse if more plies are considered (Fotland, 1996).

MFG uses caching to reduce the amount of time spent reading. Since strings are read twice, tactical results related to eyes, capture or threat, and cuts are cached rather than re-evaluated. Life and death analysis are cached as trees since they are smaller than the trees which would result from tactical searches (Fotland, cgm4 16 Aug. 1994).

Influence Function

The influence function radiates influence which is inversely proportional to distance. Influence is radiated to a fixed maximum distance of nine although when lower playing levels are chosen, the distance is smaller. Stones and connection impede the radiation of influence. Black and White influence are radiated separately (i.e, they are not summed together to give a single value for each board point) so that their relative values can be compared. Dead stones radiate negative influence and thus, since Black and White influence is maintained separately, dead stones reduce their own influence rather than increase their opponents influence. The initial influence value radiated from a stone depends on its strength.

Influence is not used to determine group connectivity. The use of influence in MFG includes determining thickness and territory, identifying surrounded groups, and generating moyo building or reducing moves. Another way in which influence is used is to determine a group's running ability. A group's ability to run towards a liberty depends on the relative values of friendly and unfriendly influence nearby. The sum of a group's ability to run toward each of its liberties determines its running ability whilst the gradient of the influence determines the direction in which it should run.

Evaluation

Board positions are evaluated in a multiple pass process. The evaluation function consists of many components which include the tactical analyser and evaluators for connections, eyes, group strength, and territory. A score for the position being evaluated is achieved by assigning a value between -50 and +50 to each board point to indicate the level of Black or White control exerted on them. The overall score for the board position is the sum of these values for each board point.

In order to try and overcome the difficulties associated with the horizon effect, Fotland chose to use quiescent search rather than modify the evaluation function. In quiescent search, positions are evaluated when they become quiet rather than when they are in a state of flux (e.g., such as in the middle of a piece exchange in chess). Positions which are not quiet are characterised by oscillations in the evaluation values returned for successive moves which makes it difficult to make good decisions based on the evaluations. MFG uses quiescent search as part of the evaluation function for full board evaluation to overcome this problem by either calling itself recursively (i.e., generating further moves) until a position becomes quiet or by using patterns suggested as obvious local answers to make the position quiet. MFG will generate up to six plies of moves in a quiescent search which improves its performance by up to four stones (Fotland, cgm1 30 Sep. 1993).

Move Suggestion

Moves are suggested by a rule-based expert system and include fuseki (e.g. shimari, kakari, and joseki moves), moves on the edge (e.g., invasions and extensions), playing in the centre, conservative play when ahead, risky play when behind, pattern matching (e.g., cutting and connecting, surrounding and escaping, invasion and defence, endgame, killing and saving groups, and shape-based moves), group defensive moves (e.g., making eyes, running, and fighting semeais), contact fights (e.g., blocking, extending for liberties, and hane), ko threats, and dame.

A limited form of full board lookahead is achieved by storing move sequences in the pattern and joseki databases. Move sequences attached to patterns in the pattern and joseki databases are played onto the board and evaluated at their endpoints. Thus if a particular joseki is suggested as appropriate, the stones in that sequence are played and the resulting board position is evaluated. This enables MFG to "play" to the end of a lookahead sequence and minimax the score returned by the evaluation function for the resulting board position.

Pattern Database

Each pattern in the pattern database has a a move tree associated with it. The pattern database contains around 1200 patterns of size 8x8 and around 6900 suggested moves with the average number of moves stored for each pattern being about 5.

Each point in a pattern is marked as black, white, empty, white or empty, black or empty, black or white, or anything (i.e., do not care). Patterns are categorised according to whether they are in the middle of the board or whether they contain edges and/or corners.

A successful match of a pattern depends on both matching the stones in the pattern with those on the board and matching any attributes associated with the pattern. Each pattern has as many as 10 attributes which pertain to stones and include whether they were dead or alive, minimum number of liberties, and connectivity between stones.

To match over a 1000 patterns on a 19x19 board in 16 different orientations requires around 3 million primitive operations. Since performance is a big issue, the patterns are compiled into a bit array which facilitates fast bit-parallel comparisons. By using an 8-bit hash function and bit-wise operations, the number of primitive operations is reduced to around 350000. This number of operations still takes enough time to make it too expensive to match all patterns more than once per move.

Patterns from the pattern database are evaluated after being played on the board in their entirety i.e., they are evaluated at the endpoints of their move trees. A small subset of patterns are used to read local sequences based on shape. Fotland has recently begun evaluating the strength of one point jump connection using patterns (Fotland, 1996).

A fast pattern matcher is necessary for a strong Go program according to Fotland. Pattern matching can be used to suggest and sort moves, and to classify connections and eyes. Reading is employed to determine whether eyes are false. Pattern matching on its own is not adequate for life and death and group strength determination (Fotland, cgm1 8 Apr. 1993). The eye and connection patterns are hand coded decision trees.

One method that Fotland tried to increase the number of patterns in the pattern database was to take them from professional games.When replaying a professional game, if MFG didn't consider the move played by a professional or the move played was low on the suggestion list, Fotland would manually cut-and-paste an 8x8 section from the game into the pattern database using a self-written graphics pattern database editor. Fotland discontinued this method since most of the missed moves were tactical (i.e., based on read-out not shape) or depended on a larger context than the 8x8 section that was placed in the pattern database. Fotland found that the cut-and-paste approach to patterns was more profitable from even games played on the IGS (Fotland, cgm1 13 Jan. 1994).

Joseki Database

The joseki database contains around 45000 moves. Joseki sequences are stored as directed acyclic graphs (i.e., they contain no loops) having empty corners at their roots. Moves in a joseki sequence can be one of several types including urgent, complex, trick, and bad. The urgent move have priority whilst the complex and trick moves are only played if MFG is behind. The bad moves are not for the program to play, rather they are used by the program to know how to respond to bad moves played by its opponent.

Joseki patterns are evaluated by being played on the board in their entirety and evaluating the resulting board position. MFG selects joseki sequences that are appropriate given the status of the other corners (Fotland, 1993).

Strategy

A strategy function is used to focus attention on important areas of the board before each move (Fotland, 1993). The dynamic data is examined to determine what phase the game is in, the relative score, the value of taking sente, and whether there are any urgent offensive or defensive moves that need to be made.

Urgent offensive and defensive moves are examined initially and if sufficiently urgent are played without any further considerations. Urgent moves can be suggested by the pattern matcher or by examination of groups which are determined to need urgent attention. Friendly groups which need urgent defence include big groups and cutting groups. Opposition groups which need urgent attack include big groups, cutting groups, and groups adjacent to friendly groups needing urgent defence.

Move suggestion is affected by the phase that the game is in. Certain rules will only fire in certain phases of the game. The fuseki phase lasts until joseki sequences have been pursued in all the corners. The middle game lasts until at least move 120 and MFG enters the end game when there are no unsettled groups on the board. Transition between middle game and end game phases may occur many times during a game.

The types of moves suggested are also affected by the relative score. MFG plays more conservatively when it is far ahead of its opponent and makes unsound invasions when it is far behind its opponent. The relative score is classified into many states including "way ahead" (over 40 points), "ahead (20 - 40 points), "about even", "behind" (over 10 points), and "way behind" (over 20 points).

Move Selection

Since the evaluation function is very slow (Fotland, cgm4 16 Aug. 1994), a limit is placed on the number of full board evaluations which can be performed each move depending on the playing level. MFG can only look at 5 to 10 moves in detail (depending on playing level) before selecting the move it finally plays. A safeguard against errors in the evaluation function is that only reasonable moves are suggested for full board evaluation (Fotland, 1993).

By employing the strategy function, the move suggestion expert system, and the joseki and pattern databases, MFG fully examines a small number of moves, playing the one which receives the highest score from the evaluation function.

The score returned from a full board evaluation is also modified by the addition of sente if applicable. Thus if MFG plays a sente move, the value of sente is added to the evaluation for the resulting position. The value of sente varies from 7 points during the fuseki to 1 or 2 points in the endgame and is determined by the strategy function.

Size, Performance and Timeline

With some help from Ishi Press and a professional artist, Fotland rewrote Cosmos' user interface and released it as MFG in 1990. Until the present time (July 1996), MFG has had 3 releases with various improvements. MFG contains around 40000 lines of C code with around another 20000 lines of user interface code.

MFG has performed well in various world computer Go championships including 4th in 1993, 2nd in 1994, and 3rd in 1995. According to Fotland, MFG gains about one stone in strength each year (Fotland, 1996). MFG plays on both the IGS and the NNGS as ManyFaces. MFG participates in the NNGS rating scheme and was rated 9 kyu (as at July 1996). It was also awarded an 8 kyu diploma from the Nihon Ki-in in Japan based on its performance against a 1 dan amateur at 9 stones and a sample play against a professional in September 1995 (Fotland, 1996).

4.2.2 Go4++

Micheal Reiss started writing Go programs in 1983 and his current program, Go4++, has evolved from various predecessors over that time. Reiss has met with some success in computer Go competitions and Go4++ came 2nd in both the 1st and 2nd FOST cups.

Reiss' programming philosophy is to use simple algorithms on a large amount of data rather than complex algorithms on a small amount of data. Go4++ calculates everything from first principles; complex concepts are calculated from simpler concepts which are in turn functions of even simpler concepts. Thus, Go4++ does not have an elaborate rule-based expert system at its core. A positive consequence of this approach is that Reiss' relatively weak ranking (2 kyu) compared to other top Go programmers is not a deficit. It also means that Go4++ usually responds well to the strange moves (by human standards) that are quite often played by computer Go programs and which are difficult to foresee when designing a rule-based system. The major drawback of this approach is that it is computation intensive and requires a powerful computer.

At the foundation of Go4++ is a massive amount of connectivity data from which almost everything else is eventually derived. Go4++ selects a move by first generating about 50 candidate moves that are analyzed by an evaluation function which estimates territory. The move scoring the highest evaluation is played as the next move. Thus, Go4++ uses 1 ply global lookahead although tactical lookahead and search is used in evaluating each move.

4.2.2.1 Candidate Move Generation

Candidate moves are generated by a process of pattern matching to determine the best 50 moves to examine in depth. Go4++ has around 15 high level patterns which include terms for the probability of an eye, safety, and territorial value. Whenever a match is made, the board point(s) suggested as good places to play have an appropriate value added to them. The 50 highest scoring board points are then examined by the evaluation function. The board point which receives the highest score from the evaluation function is played as the next move.

In some circumstances, Go4++ effectively evaluates more than 50 candidate moves per turn. Pattern matching is not applied to regions of the board where the stone safety (see Stone Safety in section 4.2.2.2) and territory (see Territory in section 4.2.2.2) do not differ from those of the previous move. Thus after evaluating the 50 highest scoring board points after pattern matching, the next move is selected from the combined set of evaluation scores of the 50 board points just considered and the evaluation scores of any board points in the undisturbed regions which were considered during the selection of the previous move.

4.2.2.2 Evaluation Function

The evaluation function is a six step process: 1. a connectivity probability map is generated, 2. groups are determined, 3. eye space is determined from which individual eyes are identified, 4. the safety of each stone is determined, 5. a radiation function combines the stone safety data and connectivity probability map to radiate safety to empty points, and 6. territory is determined. Reiss describes the evaluation function as pessimistic since whenever it is applicable, the evaluation function considers that the opponent is the next to move.

Connectivity Probability Map

Each time a hypothetical move is played on the board, a connectivity probability map for all friendly and opponent stones (including the hypothetical stone) is generated and stored. The connectivity probability map for a stone contains the probability of connecting to nearby friendly stones already on the board or to an empty point if it was occupied by a friendly stone. Stones and empty points which can be reached directly (nobi), by a diagonal move (kosumi link), a one point jump (ikken-tobi link), a two point jump (nikken-tobi link), a small knight's move (kogeima link), or a large knight's move (ogeima link) are examined (total of 32 possible points).

The probability of connecting two stones is calculated empirically by playing out the sequences of moves needed to determine whether the stones can be connected or whether the opponent can cut them. This process requires the use of lookahead, particularly when ladders are generated by cutting moves (e.g., cutting a kogeima link generates two ladders, one for each cutting point). If all possible cutting stones are captured, then the probability of connection is 100%. However, if the cutting stones can not be captured, a hand-tuned algorithm estimates the connection probability.

A massive amount of data is generated in calculating the probability map for each stone on the board for every hypothetical stone being evaluated. The process is very computationally expensive and requires a powerful computer (Go4++ currently runs on a Pentium-Pro 200).

Group Determination

Stones and strings are catalogued into groups: any stones which are 100% connected are considered groups. A tactical search on all strings with less than 4 liberties is used to determine which strings are definitely dead. Dead strings are not included as part of any group.

Eye Identification

Identifying eyes is achieved in a two step process: 1. eye space is determined, and 2. individual eyes are identified from the eye space.

A floodfill type algorithm is used to identify contiguous regions in which opponent connectivity probability is low. Points in those regions whose 8 neighbouring points are mostly clear of opponent connectivity probability are considered to be eye space.

Individual eyes within a groups eye space are identified by shape. There are several grades of eyes with the grade being a function of the opponent's connectivity map. Eyes with a grade above a certain level (see Stone Safety below) are considered to be true eyes.

Stone Safety

The safety of each group is determined by the number of true eyes it has. The safety process is repeated 5 times; each successive pass is more pessimistic about which points will eventually become true eyes (i.e., the threshold is raised for selecting which grade of eyes will eventually become true eyes). The final safety value for a group is the average of its safety scores on each of the 5 passes.

Radiation Function

The safety value for each stone is radiated to the nearby empty points in proportion to the connectivity probability map for that stone. The inverse of a stones safety (100% - safety) is radiated in the same manner and contributes to the opponents radiated value i.e., dead stones radiated full opponent safety. Black and white radiation (including inverse radiation) is summed at each empty point.

Territory

Black and white territory is estimated from the radiation values of the empty points. The difference between black and white territory is returned as the evaluation of the hypothetical move for which it was generated.

4.2.2.3 Performance and Timeline

Reiss' Go skill has progressed from 10kyu in 1987 to 4 kyu in 1992 to 2 kyu in 1996. Reiss has programmed full-time on Go4++ for about the last year (1996) and also programmed full-time for one and a half years around 1986. Other than for these two periods since starting Go programming in 1983, Reiss has programmed part-time with the most effort usually expended in the two months leading up to a competition.

There have been many commercial releases of Reiss' programs by Oxford Softworks with another soon to follow. Notable releases have been Go Player Professional and an updated windows version, Go Professional II, released in Japan.

Reiss characterized Go4++ as the weakest of the current strong programs at tactical situations requiring life and death analysis although it is good at creating moyos and gaining territory in the middle and endgame. Since Go4++ tends to play well in the centre of the board, Prof. Chen played 200 games against Go4++ in an attempt to test modifications to Handtalk which were designed at playing better in the centre.

According to Reiss, other weaknesses are the absence of global lookahead, lack of a concept of "shape", and the reluctance of Go4++ to invade. Since the evaluation function pessimistically considers that the opponent moves next during tactical searches, Go4++ does not usually evaluate the likelihood of invading stones forming eyes as being favourable. To compensate for not invading well, Go4++ always plays it first move at the 3,3 point and also tries to live in as many places as possible to stop its opponent creating moyos early.

Reiss uses many empirically hand-tuned algorithms within Go4++ although no learning algorithms are used. Carefully crafted changes to these algorithms can improve the strength of Go4++ e.g., by making the connection algorithm more accurate, eye and territory evaluation also become more accurate, resulting in an increase in playing strength. Before the 2nd FOST Cup in 1996, Reiss tuned the performance of Go4++ by playing 700 test games against Handtalk, resulting in Handtalk's only defeat during that competition.

4.2.3 Handtalk

Handtalk has been one of the strongest programs in recent years and is written by Zhixing Chen, a Chinese professor from the University of Guangzhou. Although Handtalk becomes stronger each year and was awarded a 4 kyu diploma by the Nihon Kiin in 1996, Prof. Chen does not believe that Go programs will reach shodan by 2000 if shodan is taken at its international level (2 - 3 dan Japanese).

Details of the architecture and algorithms used by Prof. Chen are not abundantly available. Some of the details which have emerged from discussions that various people have had with Prof.Chen at various competitions are provided below.

Handtalk is written completely in IBM-PC assembly language and is very small (around 250k) and very fast. Only a very small number (around 4) candidate moves are evaluated using a static evaluation function which seems to be accurate and stable. Handtalk also uses an influence function whose influence decreases as 1/2^distance.

Handtalk does not use very much global search. Pattern matching is used to some extent although it is unclear whether the patterns are contained in a database or if the pattern matching is rule-based. Handtalk does not use joseki much and has only about 10% as many josekis as MFG.

According to Prof. Chen, Handtalk's strong points are its fighting, group safety estimation, ability to recognize life and death, the end game, and board evaluation. Other people have also commented on its strength at estimating a group's running ability, sense of shape, the middle game, and winning semeais. Prof. Chen characterizes its weaknesses as surrounding, ko, and attacking territory. Recent changes include fighting less often than in previous versions and an improvement in gaining territory in the centre which was achieved by testing alterations in around 200 games played against Go4++.

4.3 Computer Go Competitions

There are various computer Go competitions throughout the world including the United States Computer Go Championship, the North American Computer Go Championship, the Computer Go European Championship, and the International Go Contest. There is also a computer Go competition conducted as a part of the Computer Olympiads held in England.

%A cash prize of around $6000 is offered to the winning program in the World Computer Go Congress as well as the chance of challenging dan ranked junior opponents to win the Ing prize. The challenging program plays 3 junior players (ages 11 - 13) which are ranked around 3 to 6 dan.

4.3.1 The Ing Prize

%Acer Incorporated and the Ing Chang-Ki Wei-Chi (Go) Educational Foundation have been joint sponsors of the International Computer Go Congress since 1985 (Shih, 1989) and also sponsored the First Computer Olympiad in 1989. The three top contestants from the North American; European; and Japan and Asia-Pacific region are invited to the International Go Congress in Tapei. A prize of approximately $1.5 million US will be won by the programmer(s) of the first program to beat a nominated human competitor without handicap on a 19x19 board. This prize is known as the Ing prize.

5.0 What's in a Go Program

6.0 Performance of Current Programs

6.1 Program versus Program Performance

6.2 Program versus Human Performance

The strongest Go programs currently play at around 8 - 13 kyu against human opponents. Ranking a program can be difficult due to the fact that human players can modify their playing style to take advantage of the weaknesses of a program. Thus it is possible for a program to play an even game with a 5 stone handicap against a 5 kyu at first and then need 8 or 9 handicap stones after a few games.

The winning program in the 1994 World Computer Go Championship, Go Intellect, lost all 3 games against the youth players on a 15 play handicap. As explained in section p.1, the Chinese rules allow the handicap stones to be placed at the players discretion. Thus a 15 play handicap means that Black (the program) places 15 stones and then plays first, in effect giving Black 16 stones before White plays. In the 1991 World Computer Go Championship, Goliath, beat all 3 of its 5 dan opponents at 16 play handicap and then lost to all 3 of its opponents on 14 play handicap.

7.0 Future Improvements in Performance

8.0 Go and Computer Go Resources on the Internet

(This section has been adapted from Accessing Go and Computer Go Resources on the Internet which will be published in the proceedings of the Second Games Programming Workshop in Japan. Various paragraphs in this section have been adapted and modified from the README file at bsdserver.ucsf.edu/Go and from the Go FAQ. Due to the nature of Internet resources, the availability of any given resource listed in this section cannot be guaranteed.)

Researchers in the computer Go field as well as individuals involved in implementing Go programs for recreation or profit can benefit from resources available on the Internet. This section provides a guide to accessing the resources that may benefit those in the computer Go field.

8.1 Computer Go Related Internet Resources

8.1.1 Anonymous FTP Archive and Mirror Sites

The main Go FTP archive site and its mirror sites contain a comprehensive archive of Go and computer Go material which is freely available by anonymous FTP. The README file in the Go directory contains a comprehensive listing of the files in the Go directory and its sub-directories as well as a brief description of each file. Below is a list of the subdirectories of the Go directory along with a brief description of their contents which has been adapted from the README file:

aga            American Go Association Files. 

clients        Clients for the Internet Go Server. 

comp           Information about programming computers to play go, and

               various attempts to do so

games          Commented games, and other specially formatted material. 

igs            Games from the IGS, in Postscript or Smart-Go. 

info           Informational files in plain text format. 

mgt            Versions of MGT, a program for reading and writing 

               Smart-Go files.

printing       Programs and files related to printing out go boards 

               and diagrams. 

pro             Uncommented professional games. 

problems       Go problems, mostly in Smart-Go format. 

prog           Programs related to go but which don't attempt to play the game.

The contents of the comp directory include:

Public domain games for the Amiga, Macintosh, IBM PC (DOS and Windows), 

        Linux, and X windows.

Archives of the computer-go mailing list.

Computer Go bibliography.

People and programs in computer Go.

Various reports, papers and theses on Go programs or computer Go issues.

Main FTP Site:
bsdserver.ucsf.edu/Go

Mirror Sites:
ftp.pasteur.fr/pub/Go
rzis1.rz.tu-bs.de/pub/go
igs.nuri.net/Go

8.1.2 The Internet Go Server (IGS)

The Internet Go Server (IGS) provides a means for people to play real-time interactive games of Go against other people or against Go programs over the internet. The IGS serves as a virtual Go club which is particularly useful for players who do not have local access to other Go players or a Go club.

First time users can login as "guest". Full access can be gained by registering for an account. Information about registering can be obtained by typing "help register". The help command provides information on how to use the interface. Once logged on to the IGS, you can play a game against another player, watch games in progress, or even comment on games in progress.

Interfacing to the IGS can be difficult and as a result, client programs have been written for various platforms e.g. Atari ST, Amiga, Macintosh, NeXT, MS Windows, IBM PC, Unix (ASCII) and X11.

Client programs available in the clients directory:
bsdserver.ucsf.edu/Go/clients/

Help on client programs:
www.well.com/user/mmcadams/igs.howto.html (follow the "getting software" link)

Help files on using the IGS:
bsdserver.ucsf.edu/Go/igs/igs_ug.ps.Z
bsdserver.ucsf.edu/Go/igs/igs_ug.txt.Z
bsdserver.ucsf.edu/Go/igs/igshelp.Z
www.well.com/user/mmcadams/igs.howto.html
ltiwww.epfl.ch/~warkent/go/etiquette/et.html

Telnet connection to the IGS:
igs.nuri.net:6969
hellspark.wharton.upenn.edu:6969

8.1.3 Game Record Formats

Several game record formats exist although currently the two most commonly used are Smart Go Format (SGF) and Ishi "Standard" Format. Information, executables, converters etc. related to game record formats can be found in the info, mgt and prog directories of the FTP archive sites.

bsdserver.ucsf.edu/Go/info/
bsdserver.ucsf.edu/Go/mgt/
bsdserver.ucsf.edu/Go/prog/
www.cwi.nl/~jansteen/go/games/SGF/sgf.html

8.1.4 The Computer-Go Mailing List

The computer-go mailing list is specifically designed as a forum for discussion about programming Go and related issues. E-mail messages sent to the list are distributed to members of the mailing list.

Many individuals involved in the computer Go field either for recreation, profit or research converse with each other via the mailing list. The types of discussions vary from abstract to implementation related. The mailing list is a good source for inspiration and new ideas, information about approaches to programming Go that have been tried and have failed, constructive criticism on ideas by others involved in programming Go, information about tournaments and results, and much more. Archives of old and current messages are also available.

The computer-go mailing list can be joined by sending an subscribe message by e-mail to:
computer-go-request@comlab.oxford.ac.uk

Past messages archive:
bsdserver.ucsf.edu:/Go/comp/ (compgo-mail-*.Z)

Current messages archive:
ftp.comlab.ox.ac.uk:/pub/Documents/computer-go/mail-archive

8.1.5 The Computer Go Ladder

Discussions on the computer-go mailing list resulted in the establishment of an informal competition between computer Go programs called the Computer Go Ladder. The primary purpose of the ladder is for the enjoyment of the participants with the secondary purposes of stimulating both interest and work on computer Go programs and providing a way of measuring the state-of-the-art of current programs.

There are HTTP links from the Computer Go Ladder page to pages related to some of the programmers and some of the programs involved in the Computer Go Ladder, world computer Go competition results, the IGS and various other associated pages on the Internet. The Computer Go Ladder is maintained by Eric Pettersen (pett@cgl.ucsf.edu).

cgl.ucsf.edu/go/ladder.html

8.1.6 Computer Go Competitions/Tournaments and Results

Various computer Go competitions/tournaments exist and some of their results are available on the Internet.

nobi.ethz.ch/martin/cgresults.html (Martin M�ller)
www.reiss.demon.co.uk/webgo/gores.htm (Michael Reiss)

8.1.7 Computer Go Bibliographies

There are several sources of computer Go bibliographies available. Peter Lipp compiled a bibliography of books, articles, theses etc. pertaining to Go, computer Go and game related issues e.g. complexity etc. Michael Reiss advertised for computer Go references on the computer-go mailing list and has compiled three WWW bibliography pages. Martin M�ller and Jay Burmeister have placed the computer Go bibliographies resulting from their PhD work on WWW pages.

igs.nuri.net/Go/comp/compbibs.Z (Peter Lipp)
nobi.ethz.ch/martin/references.html (Martin M�ller)
www.reiss.demon.co.uk/webgo/bib.htm (Michael Reiss)
www.psy.uq.edu.au/~jay/go/comp-go.bib.html (Jay Burmeister)

8.1.8 Game Databases

The IGS game archive contains games played on the IGS archived in postscript and Smart Go formats. Jan van der Steen is involved in a Go database project, GoBase, which is designed to allow thousands of professional Go games to be searched.

igs.nuri.net/Go/IGSArch/ (IGS archive)
bsdserver.ucsf.edu/Go/games/
bsdserver.ucsf.edu/Go/pro/
imageek.york.cuny.edu/search5d.html (5+ dan IGS games)
www.cwi.nl/~jansteen/gobase/gobase.html (Go Base) www.geocities.com/SiliconValley/Park/4872/index.html

8.2 Go Related Internet Resources

8.2.1 Go Rules and Learning to Play

There are different versions of Go rules, some of which are available in various formats on the Internet.

bsdserver.ucsf.edu/Go/RULES
bsdserver.ucsf.edu/Go/RULES.SG
bsdserver.ucsf.edu/Go/aga/aga.rules.Z
bsdserver.ucsf.edu/Go/aga/ingrules.zip
bsdserver.ucsf.edu/Go/igs/goe.rules.Z
bsdserver.ucsf.edu/Go/igs/goe.on.igs.Z

8.2.2 Go Learning Aids and Tutorials

There are Go tutorials and versions of Go rules which are also designed to give novice players tutorial help in learning Go available on the Internet.

bsdserver.ucsf.edu/Go/RULES.PS.Z
www.cwi.nl/~jansteen/go/rules/human.html
www.cs.vu.nl/~willems/go.html
ltiwww.epfl.ch/~warkent/go/rules/rules.html
ltiwww.epfl.ch/~warkent/go/rules/9x9game/1.html (ASCII)
hyperg.iicm.tu-graz.ac.at/GTL (Teaching Ladder page)
Section 2 of this document

8.2.3 The Go News Group

The news group rec.games.go is a good forum for discovering and sharing information about Go, tournaments, the IGS, etc. The Go news group is not specifically aimed at computer Go, however, discussions and information related to computer Go sometimes appear on the newsgroup.

rec.games.go

8.2.4 The Go Frequently Asked Questions (FAQ)

The Go FAQ contains questions that are frequently posted to the rec.games.go newsgroup and includes sections on basic Go, the IGS, and computer Go related issues.

bsdserver.ucsf.edu/Go/FAQ
rtfm.mit.edu/pub/usenet/news.answers/games/go-faq
www.cs.utexas.edu/users/orb/go/gofaq.html

9.0 Conclusions

Appendix A Common Go Terms and Their English Equivalents

The following selection of Go terms and their English equivalents are a subset of a file (definitions.Z) available by anonymous FTP which was originally due to Fletch Holmquist and was extended by Bill Taylor.

Atari: An immediate threat to capture; a single liberty remains. A verbal warning is often issued when placing an opponent into ate.

Dame (useless): A neutral point, territory for neither; a liberty.

Dan: Advanced grade.

Fuseki: The opening moves of the game where influence and territory outlines are formed. (literally: `no stones')

Gote: Defensive play, loss of initiative. (Literally:'lower hand'.)

Hoshi: (`star point'), 4-4 point.

Ikken-tobi: One point extension.

Joseki (established stones): Known sequences of moves near the corner which result in near equal positions for white and black.

Keima: Knight's move extension.

Ko: Repetitive capture. (literally: `eternity')

Ko threat: Intervening move (that one hopes will force a reply) before a ko can be recaptured.

Komi: Score adjustment usually penalizing black for playing first. Often 5.5 points.

Kosumi: A diagonal play next to one's own stone.

Kyu: Learner grade.

Nobi (Stretch): An extension away from an opponent's tsuke, cross-cut, etc.

Ogeima (large knight's move): Three across and one vertically (or vice versa).

Seki: A situation where neither player may place the other in ate without placing himself in ate. Stalemate, with no territory awarded.

Sente: Threat forcing direct response, creates initiative. The right to choose where to play next. Opposite to gote. (Literally: `upper hand'.)

Shicho: Ladder play.

Shicho-atari: Ladder breaker. A stone played in the path of a potential shicho, threatening to make it fail.

Tobi: Jump.

Wei Chi: The Chinese name for Go. (literally:"game of encirclement")

References

(The references below are those which do not appear in the general Go Bibliography)

Berliner, H. J. A chronology of computer chess and its literature. Artificial Intelligence, 10, pages 201 - 214, 1978.

Fotland, D. The program G2. Computer Go 1, 1986.

Fotland, D. Knowledge representation in the many faces of Go. Available on the I nternet at ftp://bsdserver.ucsf.edu/Go/comp/mfg.gz, 1993.

Fotland, D. Personal communications, 1996.

Stoutamire, D. Machine learning, game play and Go. Technical Report TR 91-128, Case Western Reserve University, Cleveland, Ohio, 1991.

Computer-go mailing list references (cgm)
Fotland, D. E-mail communication on the computer-go mailing list.
Mailing list archive available on the Internet at ftp://bsdserver.ucsf.edu/Go/comp/
cgm1 compgo-mail-1.Z
cgm4 compgo-mail-4.Z