H-IFF Explained

A variety of modular tasks have been proposed to study the conditions under which GAs outperform comparable search techniques. Hierarchical-If-and-only-If (H-IFF) [16] is one such function that is hierarchical, modular, is not searchable by mutation, but is amenable to search by crossover. Its defining characteristics are two fitness peaks at opposing corners of the search space. Combinations of the sub-components that comprise each level of the competing hierarchies cause many sub-optimal peaks and consequently many local optima.

H-IFF [16] is defined on bit-strings of length 2ⁿ. The fitness value of a particular string is defined in terms of hierarchical `building blocks' which are sub-strings of the main bit-string. The building block at the highest level of the hierarchy is defined over the entire bit-string (i.e., all 2ⁿ bits). Each building block is recursively divided into two equally-sized blocks, except for blocks of size one, which cannot be divided. For a building block to be correctly set, it must consist of either all 1s or all 0s. The value of a correctly set building block of size n is 2ⁿ plus the sum of the values of its two sub-blocks (whose values depend on the sub-sub-blocks). Thus, the overall value of a bit-string of length 2ⁿ is the sum of values for the building blocks of sizes 1, 2, 4, ..., 2ⁿ. The optimal bit-strings consist of either all 0s or all 1s so that they are rewarded for building blocks of every size. The evaluation of the H-IFF function is more easily understood by way of example, shown for an 8-bit string in Fig.3.

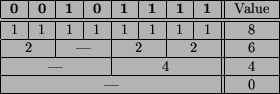
Figure 3: Evaluation of H-IFF for the bit-string 00101111 showing hierarchical decomposition. For this bit-string, H-IFF evaluates to 8 + 6 + 4 + 0 = 18. Note that the maximum obtainable value for each level of the hierarchy is 8, so the maximum value for H-IFF on bit-strings of length 8 is 32.

For H-IFF defined on l = 2ⁿ bits there will be n + 1 levels of building blocks. Within these levels there will be l/k building blocks of size k, each of which has value k. The optimal bit-strings of length l therefore have value l(n+1). The minimum value for H-IFF on bit-strings of length is l. Such a bit-string contains all building blocks of size 1 but no higher-level blocks.

The major difference between H-IFF and the more well known Royal Road function is that RR has a single optimal bit-string (all 1s) and significantly, no local optima other than the global optimum (although there are local plateaus). By comparison, H-IFF has two optimal bit-strings and, for bit-strings of length l = 2ⁿ, there are 2^l/2 local optima.