Competitive Learning
The Activation Function
The Self Organizing Map is called a competitive algorithm because
units compete to represent the input pattern. At any one time only
one of the output units is on (set to one) and all other units
are off (set to zero). The algorithm chooses the winning unit by
comparing the current input pattern against the weight vector of each of the output units. The one that is closest wins. That is, unit i wins if:
|wi - p| < |wj - p| for all j
where wj is the weight vector of the jth unit and p is the
current input vector.
The Learning Rule
Only the winning unit and its neighbours modify their weights. The change in
the weight is determined by how close the input pattern is to the unit's
weight vector, the learning rate and a neighbourhood function, which
indicates how near the unit is to the unit that won the competition.
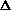 wjk =
wjk =  N(i,j) (pk - wjk)
N(i,j) (pk - wjk)
where wjk is the weight from unit k to unit j,  is the learning rate, N(i,j) is the nearness of unit
j and the winning unit i, and pk is the kth component of the
input vector.
is the learning rate, N(i,j) is the nearness of unit
j and the winning unit i, and pk is the kth component of the
input vector.
The neighbourhood function is greatest for units that are close
together (especially the same unit) and decreases as the distance
between the two units increases. It is important to realize that
neighbourhood refers to the physical proximity of the units not how
close their weight vectors are. In BrainWave, the Neighbourhood function is controlled by the MapWeights between units in the Map
layer.
These weights can be automatically set using the SetNeighbourSize Button.
The SetNeighbourSize button determines physical proximity by the
number of pixels between the units on the screen - so moving the units
will affect how much one unit is affected when a nearby unit wins the
competition for an input.
The neighbourhood function used:
N(j, k) = 1/(1 + (d(j, k) / (202 * n2))
d(j, k) = (xj - xk)2 + (yj - yk)2
where xj is the x screen coordinate of unit j, yj
is the y screen coordinate of unit j, 20 is the width in pixels of a
unit (rescaling into unit widths) and n is a neighbourhood size
parameter that can be altered to change the rate at which the function
decreases.
The Jets and Sharks Example
Figure 2: The Jets and Sharks Self Organizing Map (SOM)
In the network above (figure 1) we trained a SOM network on a set of
gang members with the intention of finding how these people cluster.
In this section, we are going to examine the solution in more
detail.
Exercise 3: Toggle the 20s, Col, Single and Pusher
units and click on cycle. Which map unit becomes active? Record the netinput values of
each of the map units. These values are the distances of each map
units weight vector from the current input. Which unit has the largest distance?
Exercise 4: Now toggle the 40s,
JH, Married and Bookie units and click cycle. Which map unit becomes active?
What is the special significance of these patterns and why do they map to
the units that they do?
Exercise 5: Select map unit 1 and click on the
Examine Weights button. The input units will now show
the weight vector associatied with unit 1. Record the pattern of
weights. Perform the same exercise for unit 5. Compare these patterns
to the patterns of activation you activated in the previous question.
Exercise 6: Complete the same exercise for the other map units. Describe
how the patterns to which each unit responds changes as you move from
map unit 1 to map unit 5.
Covering Feature Space: A Two Dimensional Example
In the previous exercises we investigated which input patterns were
captured by each of the map units. We were looking at where inputs mapped
to in the topological space of the map layer. Another way to look at
the Self Organizing Map is to plot the weight vector associated with
each of the map units in the input space. This representation allows
us to see how the map is covering the input patterns.
The input space becomes more complicated as we increase the number of dimensions (i.e. we increase the number of input units).
As a consequence we are going to consider a simple two input
- four output network (see Figure 3).
Figure 3: The Two Input Network.
The w1 and w2 values next to each of the map units show the weights going from the input units to that map unit. w1 is the weight from input unit 1 and w2 is the weight
from input unit 1.
Exercise 7: We will begin by considering the patterns in
Input Set 1. Randomize the weights and plot each of the weight vectors
(w1, w2) of the map units. You should now have a graph with four points
on it. Now, connect those units that are adjacent within the map layer. Then
train the network for five cycles and plot the weight vectors on
a separate graph. Finally, train for another 50 cycles and plot
the resulting weight vectors on a third graph. How does the plot
change as training progresses?
Exercise 8: Complete the same exercise for Input Set 2. How does the
pattern change as compared to the first input set? Examine the
patterns in Input Set 1 and Input Set 2. Why do the patterns
unfold as they do in each set?
The Development of Feature Maps
Self organizing networks like the SOM have
been used as models of how sensory maps form within human and animal brains.
In our final example, we will look at the development of an orientation map
using the SOM architecture (Figure 4).
Figure 4. A SOM network, showing the 3x3 input units, 5x5 map (or output)
units, pattern sets for input and test patterns, and output set with no
patterns.
This network has a three by three "retina" on which lines
of different orientations can be displayed. These input
line segments are then mapped to a five by five map
layer. Figure 5 shows the four input patterns on which the
network will be trained and figure 6 shows the additional patterns
on which it will be tested.
Figure 5: The Training Patterns for the Orientation Network.
Figure 6: The Test Patterns for the Orientation Network.
Exercise 9. Test the effect of the neighbourhood size by changing
the "Neighbourhood Size" parameter to 1, and cycling the first
input pattern. Remember to click on the SetNeighbourSize button
to update the map weights.
Also test for size=8.
Change it back to 4 for the next section. What changes occur when the "Neighbourhood
Size" parameter is decreased, or increased, compared to the default
value of 4?
Exercise 10. Test the effect of the proximity between output units,
by moving the top left hand unit away from the other units. Activate the
Set Neighbourhood Size button again and cycle the first input pattern.
Describe what happens to the activation of the neighbours of the
winning unit. (Be sure to set the unit back and click on the
Set Neighbourhood Size button before starting the next exercise.)
Figure 6: The Migration of Output as a function of Training.
Exercise 11: In this exercise we are going to examine how the preferred
output unit for each input changes as a function of training, filling in
figure 6 as we train.
For each of the patterns in the input and test sets, record which unit
wins the competition by writing the number of the pattern (1 -4 for the
Input patterns and 5-9 for the Test patterns) in the winning unit's square.
Record your answers on the Figure labelled "Learning=0". Note
that some map units may win the competition for more than one input pattern.
Now train the network for 4 cycles and fillin the Figure labelled
"Learning=4". Continue the exercise until you have
done 36 training cycles (and filled in Figure 6 entirely).
Describe in words the changes that are shown in the map
layer from the untrained network to the fully trained one.
Figure 7. Weights into the Map layer.
Exercise 12: In this exercise we are going to examine the weights into the map layer in a fully trained
network by filling in Figure 7. To examine the weights into a map unit select the
map unit you wish to examine and click on the
"Examine Weights" button. The input units will show the levels of activation
corresponding to the weights. This pattern of activation is the optimal
input pattern to activate that unit.
Using the fully trained network,
record the weights for each of the units in the map layer.
For this exercise, you will be looking for the patterns in the weight values,
and precise values are not required: Use a simple scheme, such as a dot
for a low weight, cross for a medium weight, and coloured square for a
high weight.
Exercise 13: What is the difference between the weights into the trained
Map layer when the top left output unit is selected compared with the bottom
right output unit. How do these differences generalize over the entire
map?
Exercise 14: Explain why the test patterns (which have received no
learning) occur in the positions that they do.
Exercise 15: Compare your map layer solutions with 3 other students in the lab (or
if you are completing this worksheet at home, randomize the weights and
repeat Exercise 12).
What differences occur in the maps created on different
trials (i.e., given different initial random weights in the network)?
Exercise 16: What similarities would you expect all trained maps (from
different initial weight sets) to show? Why?
Exercise 17: What is a "twisted map"? How could such a
map arise in the network? See if you can create a twisted map - run several
trials from different starting weights and record what proportion results
in a twisted map.
References
Kohonen, T. (1982). Self-organized formation of topologically correct
feature maps. Biological Cybernetics, 43, 59-69.
 The Connectionist Models of Cognition homepage.
The Connectionist Models of Cognition homepage.
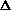 wjk =
wjk =  N(i,j) (pk - wjk)
N(i,j) (pk - wjk)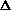 wjk =
wjk =  N(i,j) (pk - wjk)
N(i,j) (pk - wjk) is the learning rate, N(i,j) is the nearness of unit
j and the winning unit i, and pk is the kth component of the
input vector.
is the learning rate, N(i,j) is the nearness of unit
j and the winning unit i, and pk is the kth component of the
input vector. The Connectionist Models of Cognition homepage.
The Connectionist Models of Cognition homepage.