Matrices - Rank Two Tensors

The vector memory, discussed above, was capable of storing items so that at a later time it could be determined if they had appeared. A matrix memory allows two items to be associated - so that given one we can retrieve the other. Algebraically, a matrix is usually represented as a bolded upper case letter (e.g. M).

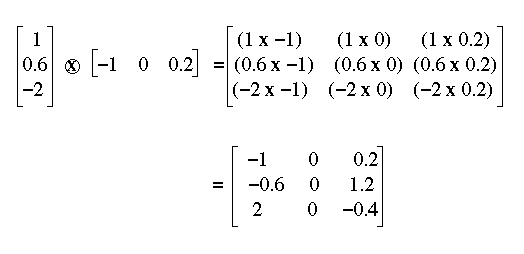
Associations are formed using the outer product operation. A outer product between two vectors is calculated by multiplying each element in one vector by each element in the other vector (see Figure 8). If the first vector has dimension d₁ and the second vector dimension d₂, the outer product matrix has dimension d₁xd₂. For instance, a three dimensional vector multiplied by a two dimensional vector has dimension 3x2.

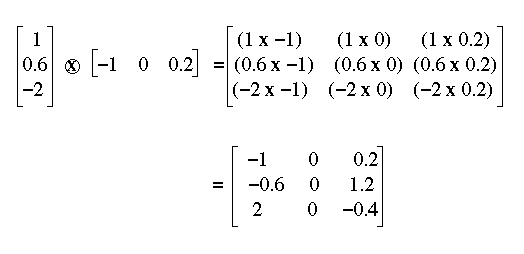
Figure 8: The outer product.

The outer product operation is expressed algebraically by placing the vectors to be multiplied next to each other. So the outer product of v and w is written as v w.

These association matrices are then added into the memory matrix (as in the vector memory case) - so that all associations are stored as a single composite. Suppose we have three people represented by the vectors a (Art), r (Rick), and s (Sam) and two gangs represented by j (Jets) and s (Sharks). Suppose that Art and Sam belong to the Jets and Rick to the Sharks. We can form a memory of these associations by finding outer products and adding:

M = aj + rs + sj

To retrieve the gang of Rick we calculate the dot product of the item vector (r) with the memory matrix.

r.M = r.(aj + rs + sj)

= (r.a)j + (r.r)s + (r.s) j

= s

since the vectors are normal and orthogonal to one another.

A matrix memory maps to a two layer network (one input and one output layer) as depicted in Figure 9. The number of input units corresponds to the number of rows in the original matrix, while the number of output units corresponds to the number of columns. Each input unit is connected to each output unit.

Figure 9: The network representation of a matrix.

In the following exercise you will use a matrix memory network to store and recall pairs of items.

Exercise 7: What rank tensor does this network implement? What are its dimensions?

Exercise 8: The items in this exercise are:

The input set contains the items FROG, KOALA and SNAIL, paired with items in the output set FLIES, LEAVES and LETTUCE, respectively. Another input item, TOAD [0.5, 0.4, 0.6, 0.45], can be used to test the network on unfamiliar input. Calculate the similarity value (i.e. dot product) of the items FROG, KOALA, SNAIL and TOAD with themselves, and each other, and record the values in the table below:

	FROG	KOALA	SNAIL	TOAD
FROG
KOALA
SNAIL
TOAD

Exercise 9: Train the network for one epoch. Test each of the items FROG, KOALA, SNAIL and TOAD. What output is produced in each case? (Give the output pattern and also describe the output patterns in terms of their similarity to FLIES, LEAVES and LETTUCE).

FROG
KOALA
SNAIL
TOAD

Exercise 10: Give the algebraic equation that describes the matrix memory formed from the three pairs of associates:

Exercise 11: Give the equations that describe each of the retrievals in exercise 9. Use the similarity measures from the table above to simplify each equation to a weighted sum of the target patterns.

Tensors of Rank Three and Above

The final sort of tensor we need to demonstrate the matrix model is the rank three tensor. The rank three tensor allows a three way association to be represented. For instance, we could store the information that John loves Mary - [Loves John Mary] - or that Apple appeared with Pencil in List 1 [List 1, Apple, Pencil].

A tensor of rank three maps to a three layer network (one input layer with two sets of units, one output layer, and one layer of hidden units) as depicted in Figure 10. The number of units in the input sets and the output set correspond to the dimensionality of the tensor. The number of hidden units corresponds to the number of units in one input set times the number of units in the other input set. Each hidden unit has a connection from one input unit from each input set, with a hidden unit existing for each possible combination. These hidden units are SigmaPi units, the value of which is set to the multiplication of the two input units to which it is connected. To implement a rank three tensor, the weights in the first layer are frozen at one. Consequently, a hidden unit's activation will equal the multiplication of the activations of the input units to which it is connected. Each hidden unit is then connected to each output unit.

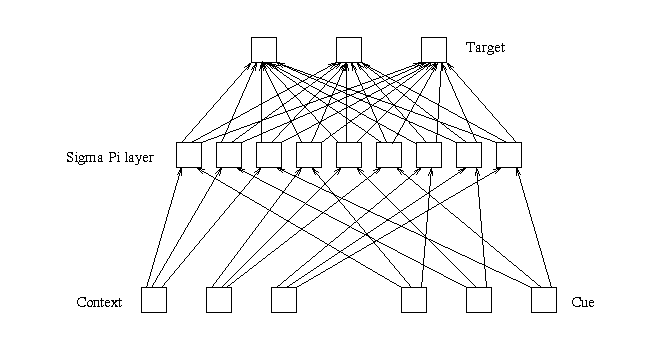
Figure 10: The network representation of a rank three tensor.

In these exercises, you will use both rank two and three tensor networks to store and recall triples of items.

Figure 11: Recalling three way information in a rank two network.

Exercise 12: The items in this exercise are:

Cues:

Relations: Targets: Notice that the vectors for the cues are the same as those used above. Also notice that EATS and LIVES-IN are orthogonal to each other - that is they have a dot product of zero.

Calculate the similarity (dot product) table for the targets.

	FLIES	LEAVES	LETTUCE	POND	TREE	SHELL
FLIES
LEAVES
LETTUCE
POND
TREE
SHELL

Exercise 13: The cue+relation input set contains the items FROG-EATS, KOALA-EATS, SNAIL-EATS, FROG-LIVES_IN, KOALA-LIVES_IN and SNAIL-LIVES_IN, paired with items in the output set FLIES, LEAVES, LETTUCE, POND, TREE, and SHELL, respectively. Two other input items, TOAD-EATS and TOAD-LIVES_IN, can be used to test the network's response to unfamiliar input.

Train the network for one epoch. Test each of the items FROG-EATS, KOALA-EATS, SNAIL-EATS, FROG-LIVES_IN, KOALA-LIVES_IN, SNAIL-LIVES_IN, TOAD-EATS and TOAD-LIVES_IN. What output is produced in each case? (Give the output pattern and also describe the output patterns in terms of their similarity to FLIES, LEAVES, LETTUCE, POND, TREE and SHELL)

Exercise 14: How does the performance of this network compare with the performance of the network in Exercise 8? Why is it not as good?

Exercise 15: Give the algebraic equation that describes the matrix memory formed from the three pairs of associates:

Exercise 16: Give the equations that describe each of the retrievals from exercise 14. Use the similarity measures from the table above to simplify each equation to a weighted sum of the target patterns.

Figure 12: Recalling three way information in a rank three network.

Exercise 17: The inputs and outputs for this network are the same as for the previous one, but the connections and hidden SigmaPi units perform different calculations on the inputs to try and achieve the correct outputs. Train the network for one epoch. Test each of the items FROG-EATS, KOALA-EATS, SNAIL-EATS, FROG-LIVES_IN, KOALA-LIVES_IN, SNAIL-LIVES_IN, TOAD-EATS and TOAD-LIVES_IN.

What output is produced in each case? (Give the output pattern and also describe the output patterns in terms of their similarity to FLIES, LEAVES, LETTUCE, POND, TREE and SHELL).

Exercise 18: Which of the two networks performs the memory task better? Why?

Exercise 19: Give the algebraic equation that describes the matrix memory formed from the three pairs of associates:

Exercise 20: Give the equations that describe each of the cued recall tests from exercise 17. Use the similarity measures from the table above to simplify each equation to a weighted sum of the target patterns.

References

Rumelhart, D. E., & McClelland, J. L. (Eds.). (1986). Parallel distributed processing: Explorations in the microstructure of cognition (Vol. 1). Cambridge, MA: MIT Press. Chapter 3: Distributed Representations.