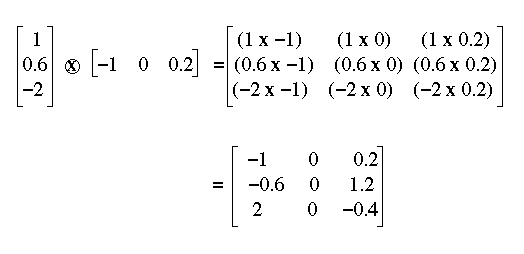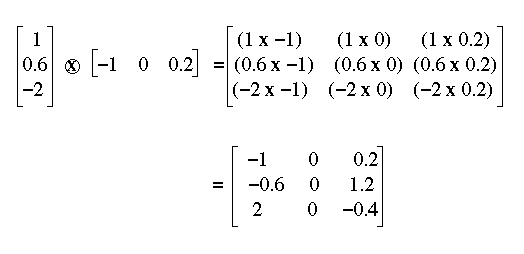[Previous] [Next]

Operations on Matrices: Outer Product

A outer product between two vectors is calculated by multiplying each element in one vector by each element in the other vector (see Figure 8). If the first vector has dimension d₁ and the second vector dimension d₂, the outer product matrix has dimension d₁xd₂. For instance, a three dimensional vector multiplied by a two dimensional vector has dimension 3x2.

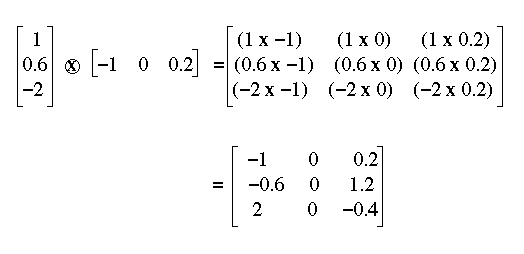
Figure 8: The outer product.

The outer product operation is expressed algebraically by placing the vectors to be multiplied next to each other. So the outer product of v and w is written as v w.